【第1回カリフォルニア住宅価格の予測】前処理無しで精度を確認
投稿日 2020年4月8日 >> 更新日 2024年7月9日
今回は有名なデータセットであるカリフォルニア住宅価格の予測を行っていきたいと思います。
このデータセットでの予測は3部作で予定しており、第1回はデータの中身を確認してどのようなタスクか、機械学習モデルの性能指標をどのようにして判断するかといった流れをざっくりですが簡単に実装します。
そして今回の実装で浮き彫りになるであろう課題を第2回、第3回、第...、と分けて住宅価格の予測精度を縮めていきたいと思います。
実行環境&使用ライブラリ¶
| 実行環境 |
|---|
| Windows Subsystem for Linux |
| Python 3.6.9 |
| pip 9.0.1 |
| Jupyter notebook |
| 使用ライブラリ | ライセンス |
|---|---|
| numpy==1.16.4 | OSI Approved (new BSD) |
| pandas==0.25.0 | BSD |
| matplotlib==3.1.1 | PSF |
| seaborn==0.9.0 | BSD |
| scikit-learn==0.21.3 | OSI Approved (new BSD) |
データセットの準備¶
まずはデータセットの準備をします。と言ってもscikit-learnを使えば簡単に幾つかのデータセットを試すことができるので、その内1つのカリフォルニア住宅価格をダウンロードします。
ついでに今回使用する全てのライブラリをインポートしておきます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
# カリフォルニア住宅価格のデータセット
from sklearn.datasets import fetch_california_housing
データを変数に格納し、中身を確認します。
# 実行
housing = fetch_california_housing()
housing
# 結果
{'data': array([[ 8.3252 , 41. , 6.98412698, ..., 2.55555556,
37.88 , -122.23 ],
[ 8.3014 , 21. , 6.23813708, ..., 2.10984183,
37.86 , -122.22 ],
[ 7.2574 , 52. , 8.28813559, ..., 2.80225989,
37.85 , -122.24 ],
...,
[ 1.7 , 17. , 5.20554273, ..., 2.3256351 ,
39.43 , -121.22 ],
[ 1.8672 , 18. , 5.32951289, ..., 2.12320917,
39.43 , -121.32 ],
[ 2.3886 , 16. , 5.25471698, ..., 2.61698113,
39.37 , -121.24 ]]),
'target': array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894]),
'feature_names': ['MedInc',
'HouseAge',
'AveRooms',
'AveBedrms',
'Population',
'AveOccup',
'Latitude',
'Longitude'],
'DESCR': '.. _california_housing_dataset:\n\nCalifornia Housing dataset\n--------------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 20640\n\n :Number of Attributes: 8 numeric, predictive attributes and the target\n\n :Attribute Information:\n - MedInc median income in block\n - HouseAge median house age in block\n - AveRooms average number of rooms\n - AveBedrms average number of bedrooms\n - Population block population\n - AveOccup average house occupancy\n - Latitude house block latitude\n - Longitude house block longitude\n\n :Missing Attribute Values: None\n\nThis dataset was obtained from the StatLib repository.\nhttp://lib.stat.cmu.edu/datasets/\n\nThe target variable is the median house value for California districts.\n\nThis dataset was derived from the 1990 U.S. census, using one row per census\nblock group. A block group is the smallest geographical unit for which the U.S.\nCensus Bureau publishes sample data (a block group typically has a population\nof 600 to 3,000 people).\n\nIt can be downloaded/loaded using the\n:func:`sklearn.datasets.fetch_california_housing` function.\n\n.. topic:: References\n\n - Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,\n Statistics and Probability Letters, 33 (1997) 291-297\n'}
中身は辞書型となっており、それぞれ「data」では説明変数に当たる数値、「target」では目的変数、「feature_names」では説明変数の各属性名、「DESCR」ではデータセットの大まかな内容となっています。
ひとまずpandasを使って必要なデータをテーブル形式のデータフレームへと格納します。
# 実行
df_housing = pd.DataFrame(housing.data, columns=housing.feature_names)
df_housing.head()
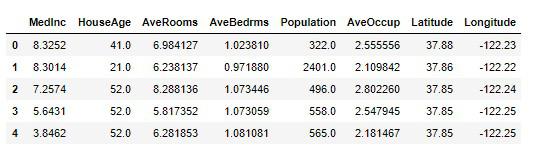
目的変数の属性名は「Price」として同じデータフレームに付け加えます。
# 実行
df_housing['Price'] = housing.target
df_housing.head()
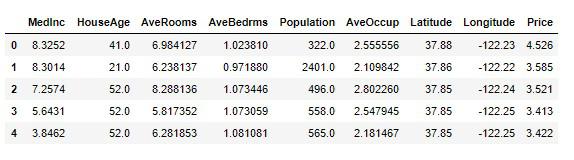
Google翻訳で訳したそれぞれの属性名やデータセットの大まかな内容を書き記しておきます。
- (MedInc)median income in block-収入の中央値
- (HouseAge)median house age in block-ブロック内の家の中央年齢
- (AveRooms)average number of rooms-平均部屋数
- (AveBedrms)average number of bedrooms-ベッドルームの平均数
- (Population)block population-ブロック人口
- (AveOccup)average house occupancy-平均住宅占有率
- (Latitude)house block latitude-家屋の緯度
- (Longitude)house block longitude-ハウスブロックの経度
The target variable is the median house value for California districts. This dataset was derived from the 1990 U.S. census, using one row per census block group. A block group is the smallest geographical unit for which the U.S. Census Bureau publishes sample data (a block group typically has a population of 600 to 3,000 people).
ターゲット変数は、カリフォルニア地区の家の中央値です。 このデータセットは、国勢調査ブロックグループごとに1行を使用して、1990年の米国国勢調査から導出されました。 ブロックグループは、米国国勢調査局がサンプルデータを公開する最小の地理単位です(通常、ブロックグループの人口は600〜3,000人です)。
ここでのタスクは、各ブロックに当たる住宅価格の中央値を予測することです。予測された住宅価格の中央値を元に、そのブロックへ投資すべきかを判断するので、その不動産屋の利益に大きく関わってくるということです。
正確な予測をさせるのであれば正確なデータが必要となってきます。
既存のデータを如何にして機械学習モデルに正しい学習をさせられるかが目的となります。
第1回目のカリフォルニア住宅価格の予測では、データを取得してから機械学習モデルで精度を確認するまでの工程だけに着目して実装します。
データの中身を確認¶
データの中に欠損値が含まれていないか確認します。
欠損値(NaN)が含まれていると、機械学習モデルでは学習できないので取り除く必要があります。
pandasデータフレームのinfo()を使うと、データの総数、各属性に対する総数、データのタイプを確認することができます。
# 実行
df_housing.info()
# 結果
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 9 columns):
MedInc 20640 non-null float64
HouseAge 20640 non-null float64
AveRooms 20640 non-null float64
AveBedrms 20640 non-null float64
Population 20640 non-null float64
AveOccup 20640 non-null float64
Latitude 20640 non-null float64
Longitude 20640 non-null float64
Price 20640 non-null float64
dtypes: float64(9)
memory usage: 1.4 MB
サンプルデータの数は20640個あり、それぞれの属性も同じ数だけあることが分かるので、欠損値は含まれていないことが分かります。
そしてfloat型、つまり全ての属性は数値データとなっています。
次に各属性の統計値を確認します。
統計値を見ることによって、それぞれにどのような特徴があるのか感覚的に掴むことができます。
# 実行
df_housing.describe()
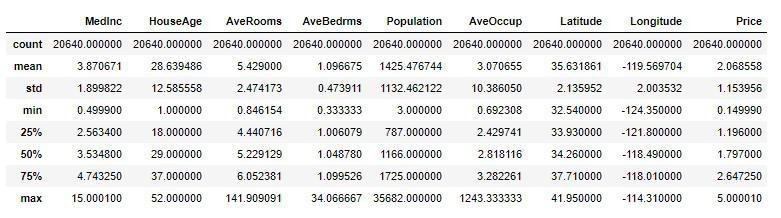
countはデータ数、meanは平均値、stdは標準偏差、minは最小値、25%は第1四分位数、50%は第2四分位数、75%は第3四分位数、maxは最大値となります。
ヒストグラムでどのように分布されているか可視化してみます。
# 実行
df_housing.hist(bins=50, figsize=(15, 13))
plt.savefig('housing_hist.png')
plt.show()
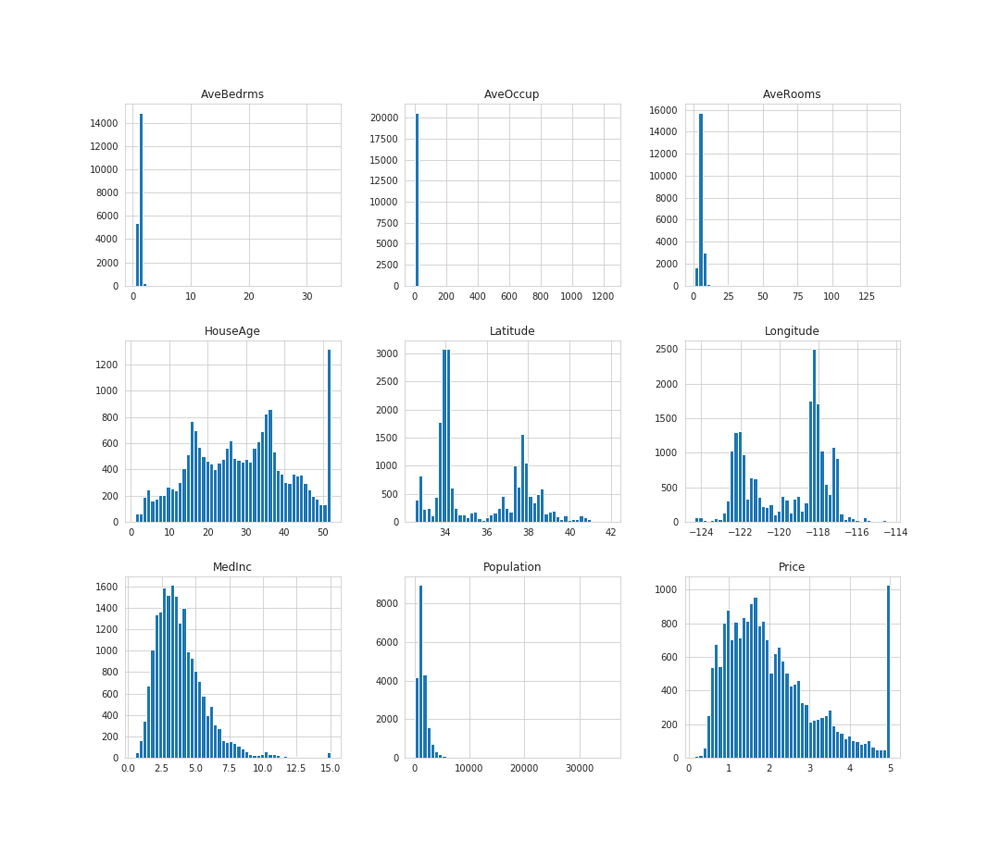
MedInc、AveBedrms、AveOccup、AveRooms、Populationのグラフに注目してみると、右側が大きく開いているのが見て取れます。
そしてHouseAgeとPriceでは最大値の数が不自然なまでに多くなっています。
このような値を外れ値と言い、機械学習モデルに悪い影響を与えてしまうといいます。
次に属性間の相関関係を見てみます。
相関関係を見ることによって必要な属性、そうでない属性を確認することができます。
# 実行
df_housing.corr()
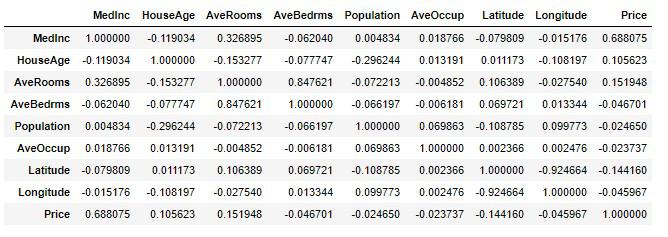
プラスに働けば正に高い相関、マイナスに働けば負に高い相関、0に近ければ相関が低くなります。
この場合は目的変数のPrice属性を軸に関係性を見ることによって、各属性に対しての影響度合いを知ることができます。
それではLatitudeとLongitudeを除いた相関図を可視化してみます。
# 実行
plt.figure(figsize=(20, 15))
sns.pairplot(df_housing.drop(['Latitude', 'Longitude'], axis=1))
plt.savefig('housing_pair.png')
plt.show()
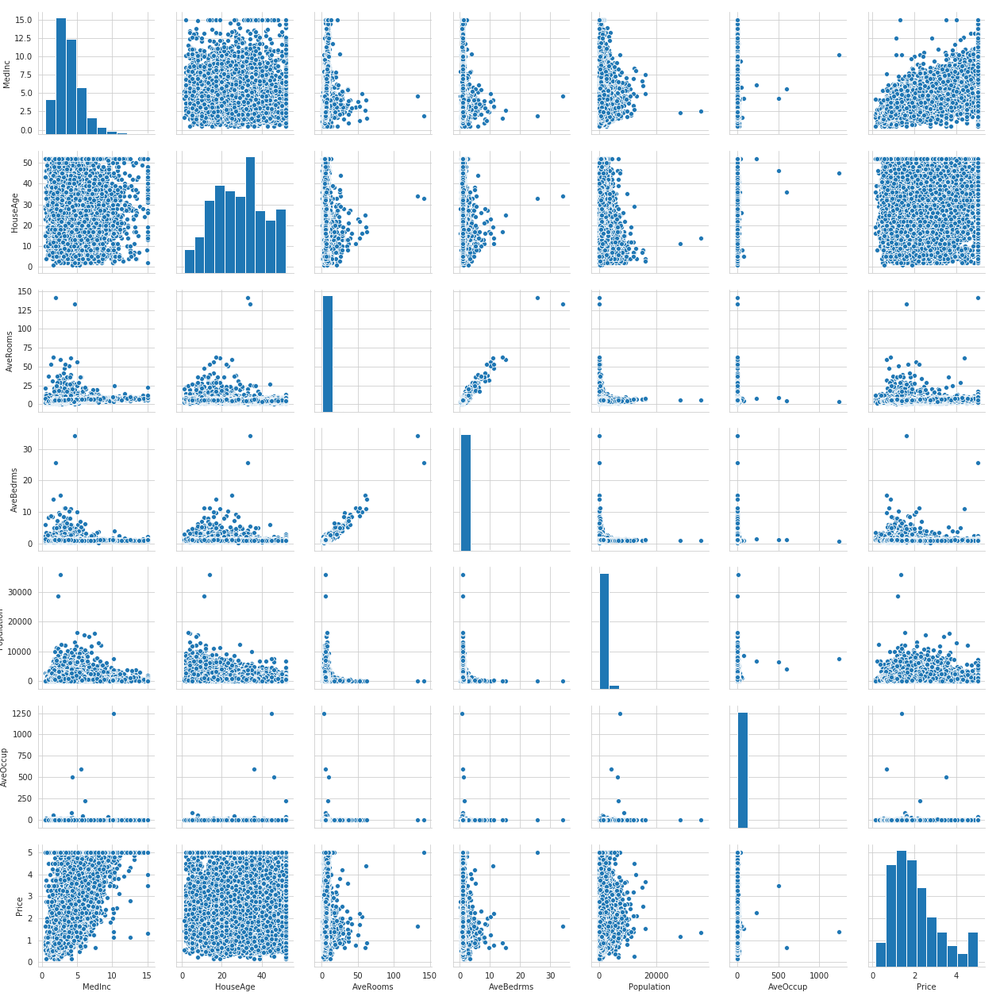
見え難くて申し訳ないですが、このように可視化することによってさまざまな知見を得ることができます。
機械学習の実装¶
機械学習モデルで訓練を行う前に、下準備をします。
まずカリフォルニア住宅価格のデータフレームを説明変数Xと目的変数yに分割します。
# 実行
X = df_housing.drop(['Price'], axis=1)
X.head()
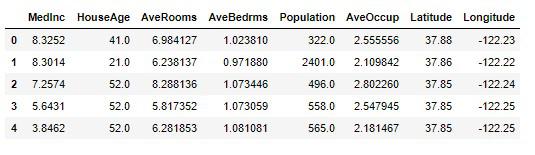
# 実行
y = df_housing['Price']
y.head()
# 結果
0 4.526
1 3.585
2 3.521
3 3.413
4 3.422
Name: Price, dtype: float64
Xとyの配列を確認。
# 実行
print(X.shape, y.shape)
Xは20640行8列、yは20640行1列となりました。
# 結果
(20640, 8) (20640,)
説明変数Xに対して、スケーリングを行います。
スケーリングは標準化とも言って、平均0・分散1にデータの散らばり具合を縮小させます。
この手法は機械学習モデルが外れ値への影響を受けにくくするためによく使われます。
標準化の詳しい計算内容に関しては第2回目で説明していきます。
scikit-learnのStandardScalerを使って簡単に実装できます。
from sklearn.preprocessing import StandardScaler
# 初期化
scaler = StandardScaler()
# データに合わせて計算しスケーリングする
X = scaler.fit_transform(X)
# もしくわ
# 後にスケーリングするために平均と標準を計算する
# scaler.fit(X)
# 計算されたデータに合わせてスケーリングする
# X = scaler.transform(X)
ここからは、訓練セット、検証セット、テストセットとなるように機械学習の精度を評価するために分割していきます。
scikit-learnのtrain_test_splitを使うと簡単に分割できます。
まずは訓練セットとテストセットを9対1の割合で分割します。
# 実行
from sklearn.model_selection import train_test_split
# random_state=42
# ランダムにサンプリングされるパターンを42に固定
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=42)
print(X_train.shape, X_test.shape)
# 結果
(18576, 8) (2064, 8)
訓練セットを使用して検証セットを8対2の割合で分割します。
# 実行
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.2, random_state=42)
print(X_train.shape, X_val.shape)
# 結果
(14860, 8) (3716, 8)
それでは準備が整ったので、さっそく訓練を行っていきます。
今回使用する機械学習モデルは、モデルの中で最も単純なアルゴリズムである線形回帰の正規方程式です。
モデルクラスをインポートしモデルを初期化します。初期化されたモデルのfit()引数に訓練セットを与えて、訓練を開始します。
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
これによりモデルパラメータが求められたので、確認してみます。
# 実行
lin_reg.intercept_, lin_reg.coef_
# 結果
(2.071587830018654,
array([ 0.83355694, 0.12763739, -0.26636753, 0.30750975, -0.00393847,
-0.04312692, -0.89406891, -0.8610534 ]))
intercept_の2.07158に当たる部分がバイアス項や切片項と呼ばれ、coef_の配列データは各属性の重みである係数となります。
これらをモデルパラメータと呼び、この数値を利用して未知のデータから予測を行います。
predict()を使うと与えられたデータから予測結果を出力することができます。
訓練セットの1部を使用して結果を見てみましょう。
# 実行
X_some = X_train[:5]
y_some = y_train[:5]
# np.roundで小数点以下3桁以降切り上げ
print('予測結果{}'.format(np.round(lin_reg.predict(X_some), 3)))
print('\n')
print('ラベル{}'.format(list(y_some)))
予測結果[1.925 1.877 0.319 4.082 2.547]
ラベル[1.027, 1.875, 0.685, 5.00001, 1.856]
ラベルである答えと比べて見ると、それとなくラベルに近づけているような予測を出していることが分かります。
予測結果とラベルとの差が小さければその機械学習モデルは最良だということがわかるので、全体的な差を求めていきます。
性能指標¶
全体的な差を求める方法は、平均二乗平方根誤差による計算方法で精度を評価します。
回帰問題では典型的な性能指標であり、RMSE(Root Mean Square Error)とも呼ばれます。
誤差の計算方法は、予測値-ラベルの二乗をし、全て足し合わせます。二乗をすることによりマイナスの値をプラスに置き換えられるので、その差の合計は全て足されることになります。
足し合わせた合計をデータの数で割り、平均値を出します。
その平均値の平方根をとることで、全体の平均±の誤差を算出できます。
$$ RMSE = \sqrt{ \frac{1}{m}\sum_{i=1}^{m} (x^{(i)} ) - y^{(i)} )^2} $$
サンプルデータが2個であった場合を例に計算してみます。
# 実行
# 予測値
x = np.array([3, 5])
# ラベル
y = np.array([6, 4])
# データ数
m = len(y)
print('予測値:{}'.format(x))
print('ラベル:{}'.format(y))
print('データ数:{}'.format(m))
# 結果
予測値:[3 5]
ラベル:[6 4]
データ数:2
実際の平均二乗平方根誤差を算出
# 実行
error = x - y
squared_error = error * error
sum_squared_error = squared_error.sum()
mean_squared_error = sum_squared_error / m
root_mean_squared_error = np.sqrt(mean_squared_error)
print('予測値とラベルの誤差:{}'.format(error))
print('誤差の二乗:{}'.format(squared_error))
print('誤差の合計値:{}'.format(sum_squared_error))
print('全体の平均:{}'.format(mean_squared_error))
print('平均値の平方根:{}'.format(root_mean_squared_error))
# 結果
予測値とラベルの誤差:[-3 1]
誤差の二乗:[9 1]
誤差の合計値:10
全体の平均:5.0
平均値の平方根:2.23606797749979
平方根を取ることで、先に二乗した値を元に戻すといったイメージです。なので、全体を平均した誤差は±2.236..という定量的な結果から精度を評価することができます。
では機械学習モデルが予測した結果の平均二乗平方根誤差を計算してみます。
# 実行
# 予測結果
lin_pred = lin_reg.predict(X_train)
# ラベル-予測結果の二乗をし合計を出す
lin_sum = ((y_train - lin_pred) ** 2).sum()
# 合計をデータの数で割って平均値を出す
lin_mean = lin_sum / len(y_train)
# 平均値の平方根をとる
lin_sqrt = np.sqrt(lin_mean)
print('誤差の合計:{}'.format(lin_sum))
print('誤差の平均値:{}'.format(lin_mean))
print('平均値の平方根:{}'.format(lin_sqrt))
# 結果
誤差の合計:7728.093485830055
誤差の平均値:0.520060126906464
平均値の平方根:0.7211519443962305
住宅価格の中央値は10万ドル単位でしたので、平均の誤差は7万2千ドルということがわかります。
scikit-leanrのmean_squared_error()を使うと、簡単に平均二乗誤差の計算を算出できます。
# 実行
from sklearn.metrics import mean_squared_error
# 予測結果
lin_train_pred = lin_reg.predict(X_train)
# 平均二乗誤差の算出
lin_train_mse = mean_squared_error(y_train, lin_train_pred)
# 平均二乗誤差の平方根を取る
lin_train_rmse = np.sqrt(lin_train_mse)
print('訓練データの誤差:{:2f}'.format(lin_train_rmse))
# 結果
訓練データの誤差:0.72115
先ほどの誤差と同じ結果となりました。
検証セットでの誤差
# 実行
lin_val_pred = lin_reg.predict(X_val)
lin_val_mse = mean_squared_error(y_val, lin_val_pred)
lin_val_rmse = np.sqrt(lin_val_mse)
print('検証データの誤差:{:2f}'.format(lin_val_rmse))
# 結果
検証データの誤差:0.723084
検証セットでもほぼほぼ同じ結果となりました。
では誤差自体は良い結果と言えるのか?
先にも述べましたが、差を0に近づければ近づけるほど良い結果と言えるので、検証セットの平均誤差7万2千ドルという値は、その誤差付近に集中しており、且つそれ以上の誤差に影響している(例えば10万ドルや20万ドル以上の誤差)と言えるので、不動産屋が投資するべきか否かを判断する材料としてはリスクが高過ぎるのではないかと思います。
よって誤差自体はまだまだ大きいですが、機械学習モデル自体は過学習を起こさずに、上手く汎化されていることが分かります。
逆に言えば、機械学習モデル自体は過小適合を起こしているので、データをクリーニングし特徴量を加えるか、別の機械学習モデルを使用して精度を比較してみる必要があります。
今回は性能指標を重点的に実装していくので、データや機械学習モデルに関しては次回以降にしていきます。
次にデータ1つ1つ誤差を可視化してみましょう。
誤差の可視化を残差プロットとも言い換えられます。
matplotlibで訓練セットとラベルの可視化
# 実行
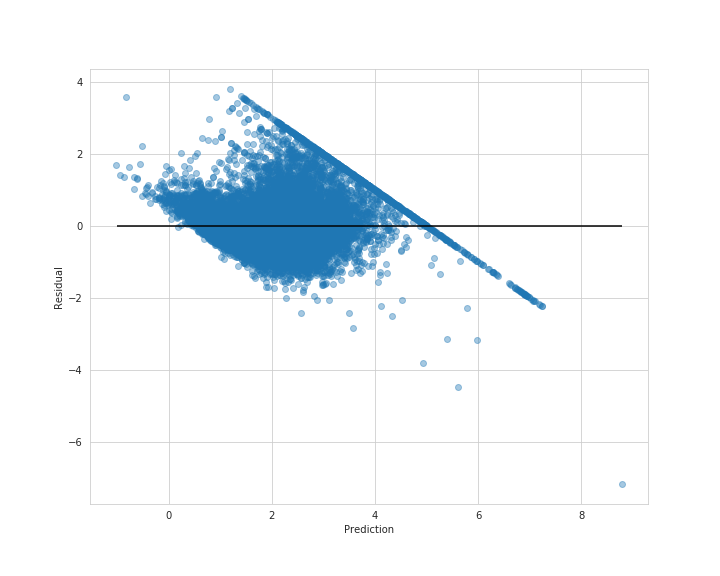
plt.figure(figsize=(10, 8))
plt.scatter(lin_train_pred, y_train - lin_train_pred, alpha=0.4)
plt.hlines(y=0, xmin=-1.0, xmax=lin_train_pred.max())
plt.xlabel('Prediction')
plt.ylabel('Residual')
plt.savefig('resid_train.png')
plt.show()
seabornを使うと簡単に可視化できます。
seabornで検証セットとラベルの可視化
# 実行
plt.figure(figsize=(10, 8))
sns.residplot(lin_val_pred, y_val - lin_val_pred, scatter_kws={'alpha': 0.4, 'color': 'red'})
plt.xlabel('Prediction')
plt.ylabel('Residual')
plt.savefig('resid_train_2.png')
plt.show()
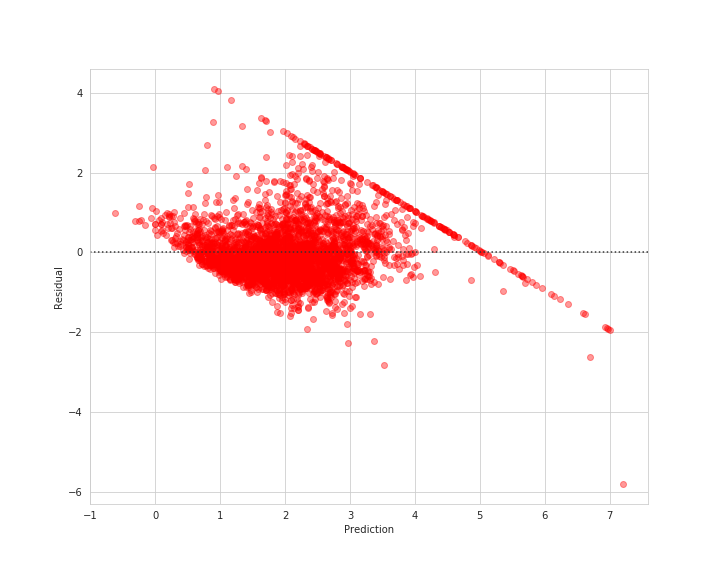
それぞれの点が0付近に集まっていれば良いですが、不平等でいて何やら斜めに線上の点が見て取れます。
このような点を分析することによって新しい知見を得ることができそうです。
# 実行
plt.figure(figsize=(10, 8))
sns.residplot(lin_train_pred, y_train - lin_train_pred, scatter_kws={'alpha': 0.4, 'color': 'blue'}, label='Train')
sns.residplot(lin_val_pred, y_val - lin_val_pred, scatter_kws={'alpha': 0.4, 'color': 'red'}, label='Validation')
plt.xlabel('Prediction')
plt.ylabel('Residual')
plt.legend()
plt.savefig('resid_train_val.png')
plt.show()
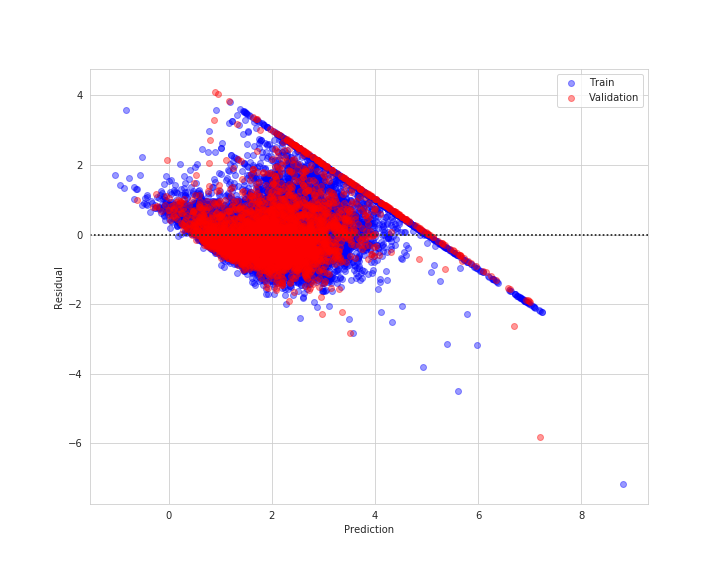
それでは線形回帰モデルでテストセットを評価し保存していきたいと思います。
すでにスケーリングを施したデータから分割していたので、そのまま予測を行い誤差を算出します。
# 実行
best_model_pred = lin_reg.predict(X_test)
best_model_mse = mean_squared_error(y_test, best_model_pred)
best_model_rmse = np.sqrt(best_model_mse)
print('テストデータの誤差:{:2f}'.format(best_model_rmse))
# 結果
テストデータの誤差:71.389959
# 実行
plt.figure(figsize=(10, 8))
sns.residplot(best_model_pred, y_test - best_model_pred, scatter_kws={'alpha': 0.4})
plt.xlabel('Prediction')
plt.ylabel('Residual')
plt.savefig('best_model_resid.png')
plt.show()
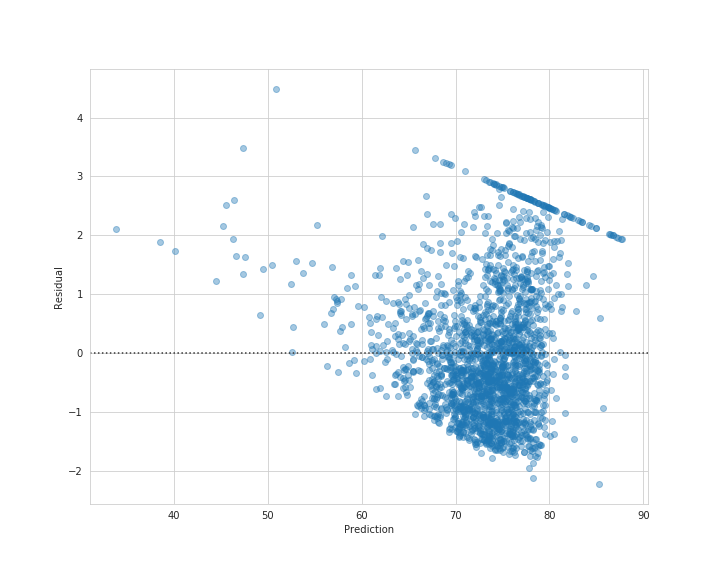
データサイエンティストが集うKaggleでもお馴染みですが、提出用に予測結果を保存します。
# 実行
submission = pd.DataFrame({
'Price': y_test,
'Prediction': best_model_pred
})
submission.head()
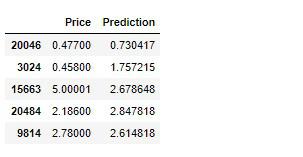
CSVファイルに保存します。
submission.to_csv('housing_submission.csv')
課題¶
今回はデータサイエンスの一連の流れを掴むために、簡単でしたがデータを取得して内容を確認し、そのまま機械学習モデルで訓練、そしてテストデータでの評価を行いました。
幸いこのカリフォルニアのデータセットは練習用として使用できることから、データの前処理を行わずにそのまま機械学習モデルに適用できました。
カリフォルニア住宅価格での課題は、未知のサンプルデータからその区域内にある住宅価格の中央値を予測し、そこへ投資するか否かを判断するということなので、より正確なデータが必要になります。
正確なデータとは、常識的であろう値であることや、外れ値といった極端にそのデータにそぐわない値の無い綺麗なデータです。
不動産に関して余り詳しくないのが現状ですが、これを機会に不動産投資に必要な要素を調べたり、データのクリーニングを行ってより正確なデータを作り出し、機械学習モデルの精度を上げることが次への課題となります。
次への課題
- データの中身をよく見る。
- 既存のデータを使用して新たな特徴量を作り出す(特徴量エンジニアリング)
- データを整える(クリーニング)
【第2回カリフォルニア住宅価格の予測】特徴量エンジニアリング&データクリーニング(データクレンジング)
それでは以上となります。
最後までご覧いただきありがとうございました。
