【第2回カリフォルニア住宅価格の予測】特徴量エンジニアリング&データクリーニング(データクレンジング)
投稿日 2020年4月15日 >> 更新日 2024年7月9日
今回は、カリフォルニア住宅価格の予測第2回ということで、特徴量エンジニアリングとデータクリーニングの実装を行っていきたいと思います。
第1回目では、scikit-leanrモジュールからデータセットの読み込みをして、データの中身をザックリ確認し、前処理などを一切行わずに機械学習モデルへ渡しました。
【第1回カリフォルニア住宅価格の予測】前処理無しで精度を確認
- データセットの読み込み
- pandasのデータフレームに格納
- データの中身をザックリ見る
- データセットを訓練セット・テストセット・検証セットに分割
- 線形回帰モデルで訓練を行う
- 正解ラベルとの誤差を確認する
- 残差プロットで当てはまりの良さを確認する
前回の結果は、訓練セットと検証セット共に予測平均誤差は約7万2千ドルでした。
残差プロットで、一つ一つの誤差がどれくらい当てはまっていたか
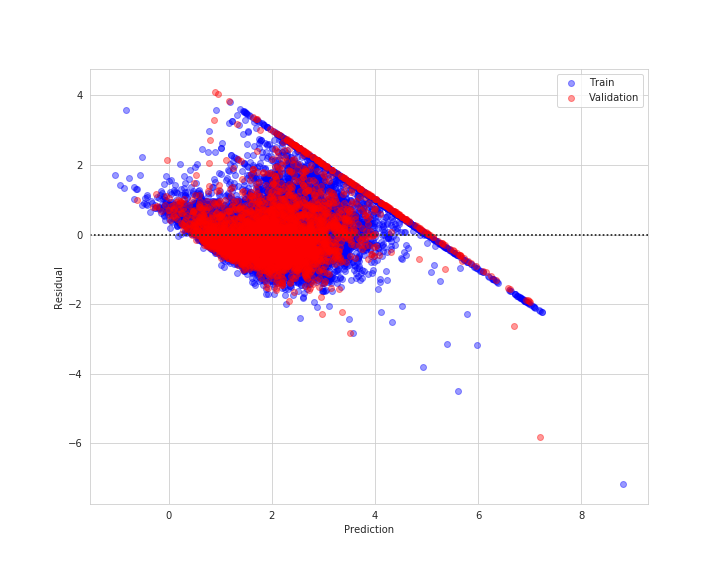
0に近ければ近いほど良い結果と言えるので、0から大きく外れていたり、線状に一定の規則があるような分布は良い結果と言えそうにないです。
このような分布を外れ値と言い、機械学習モデルがこのような外れ値への影響を受けないようにデータクリーニングを行っていきます。
また、データの属性(特徴量)を増やすことによって機械学習モデルの精度が上がる可能性もあります。このようなテクニックを特徴量エンジニアリングと言います。
これらを前処理と言いますが、人によって様々な方法やテクニックがあるのでここでの実装は参考程度に留めておいてください。
それでは第1回目で浮き彫りとなった課題を中心に実装していきましょう。
実行環境&使用ライブラリ¶
| 実行環境 |
|---|
| Windows Subsystem for Linux |
| Python 3.6.9 |
| pip 9.0.1 |
| Jupyter notebook |
| 使用ライブラリ | ライセンス |
|---|---|
| numpy==1.16.4 | OSI Approved (new BSD) |
| pandas==0.25.0 | BSD |
| matplotlib==3.1.1 | PSF |
| seaborn==0.9.0 | BSD |
| scikit-learn==0.21.3 | OSI Approved (new BSD) |
| scipy==1.3.1 | BSD |
データの前処理¶
まずはscikit-learnからカリフォルニア住宅価格のデータセットを読み込みます。
ついでに他のライブラリもインポートしておきます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
from sklearn.datasets import fetch_california_housing
データを読み込んで、pandasのデータフレームに格納します。
# 実行
housing = fetch_california_housing()
df_housing = pd.DataFrame(housing.data, columns=housing.feature_names)
df_housing['Price'] = housing.target
df_housing.head()
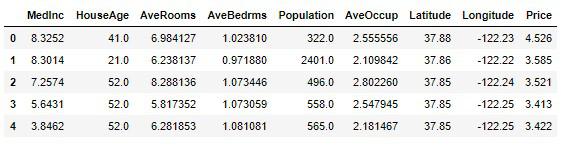
このデータを使って、今後投資していくに相応しい住宅価格の中央値を予測していきます。
- (MedInc)収入の中央値
- (HouseAge)ブロック内の家の中央年齢
- (AveRooms)平均部屋数
- (AveBedrms)ベッドルームの平均数
- (Population)ブロック人口
- (AveOccup)平均住宅占有率
- (Latitude)家屋の緯度
- (Longitude)ハウスブロックの経度
ターゲット変数は、カリフォルニア地区の家の中央値です。 このデータセットは、国勢調査ブロックグループごとに1行を使用して、1990年の米国国勢調査から導出されました。 ブロックグループは、米国国勢調査局がサンプルデータを公開する最小の地理単位です(通常、ブロックグループの人口は600〜3,000人です)。
欠損値やデータ型を調べる¶
欠損値や文字列のデータが含まれていると、機械学習では適用できないので始めに調べておきます。
# 実行
df_housing.info()
# 結果
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 9 columns):
MedInc 20640 non-null float64
HouseAge 20640 non-null float64
AveRooms 20640 non-null float64
AveBedrms 20640 non-null float64
Population 20640 non-null float64
AveOccup 20640 non-null float64
Latitude 20640 non-null float64
Longitude 20640 non-null float64
Price 20640 non-null float64
dtypes: float64(9)
memory usage: 1.4 MB
欠損値が含まれている場合データの数がRangeIndexと異なるのですべて揃える必要があります。
そしてデータ属性は全てfloat(浮動小数点数)である数値属性です。intやfloat型ではなくobjectとなっている場合は文字列として格納されているので、取り除くか、何等かの値に置き換える必要があります。
文字列型の置き換えは後ほど特徴量エンジニアリングで行う際に実装していきます。
欠損値の数を知りたい場合は、isnull()に合計値を出します。
# 実行
df_housing.isnull().sum()
# 結果
MedInc 0
HouseAge 0
AveRooms 0
AveBedrms 0
Population 0
AveOccup 0
Latitude 0
Longitude 0
Price 0
dtype: int64
統計情報の内容¶
各属性は数値属性だったので、その統計情報を確認します。
# 実行
df_housing.describe()
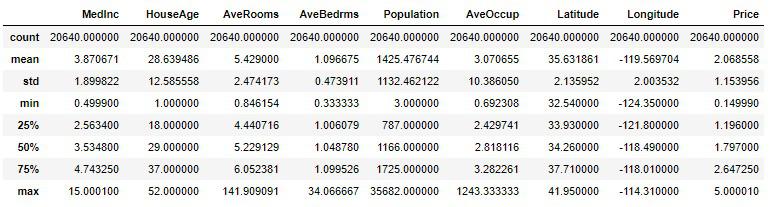
- count(データ数)
- mean(平均値)
- std(標準偏差(平均値からの分散))
- min(最小値)
- 25%(第1四分位数)
- 50%(第2四分位数(中央値))
- 75%(第3四分位数)
- max(最大値)
mean(平均値)と50%(中央値)の違いは、平均値は合計値をデータ数で割った割合なので大小に左右されやすいです。それに対し、中央値はデータの小さい順からちょうど真ん中に当たる値を指しているので、大小に左右されていない本来のデータです。
25%(第1四分位数)と75%(第3四分位数)の差は四分位範囲とよばれ、その範囲はデータ内の代表値と言えることができます。
ヒストグラムで可視化すると、そのデータの分布を確かめることができます。
std(標準偏差)は、(データ-平均値)を二乗し、その合計値をデータ数で割ると分散値が求められます。分散値に平方根をとると、標準偏差となります。
標準偏差は平均値からの散らばり具合を表しており、正規分布または確率分布によって可視化することができます。平均値から±標準偏差は68.3%、平均値から±標準偏差×2は95.4%、平均値から±標準偏差×3は99.7%の値が収まると言われています。
後ほど外れ値の処理で実装しますが、これら平均値と中央値の乖離(かいり)を無くし正規分布に従わせることで、機械学習は正しく学習を行えると言われています。
訓練セットとテストセットに分割¶
ここで一旦、訓練セットとテストセットに分けておきます。
未知のデータを作っておくことで、厳しく評価を行うことができると考えます。
scikit-learnのtrain_test_split()を使って分割します。
from sklearn.model_selection import train_test_split
X = df_housing.drop(['Price'], axis=1)
y = df_housing['Price'].copy()
# random_state=42
# ランダムにサンプリングするデータを固定する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
データの個数を確認
# 実行
X_train.shape, X_test.shape
# 結果
((16512, 8), (4128, 8))
では訓練セットとテストセットをそれぞれpandasのデータフレームに格納します。
train_set = pd.concat([X_train, y_train], axis=1)
test_set = pd.concat([X_test, y_test], axis=1)
ヒストグラムで、それぞれ均等に分割されているか確認してみます。
訓練セットを描画
# 実行
train_set.hist(bins=50, figsize=(20, 15), label='TrainData')
plt.legend()
plt.savefig('train_hist.png')
plt.show()
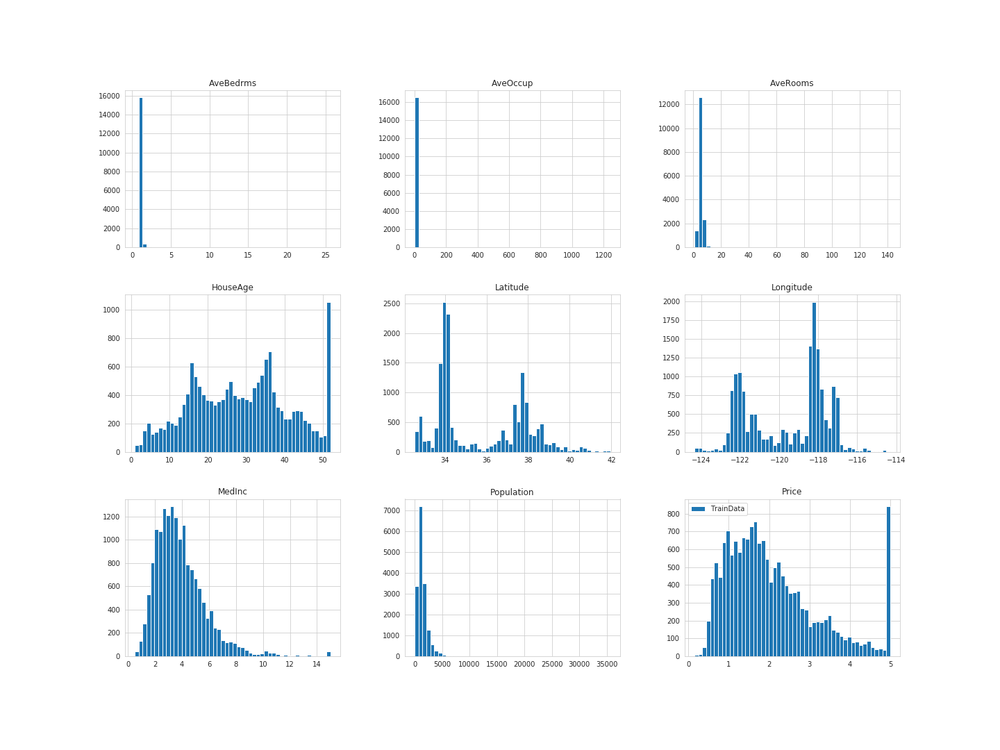
テストセットを描画
# 実行
test_set.hist(bins=50, figsize=(20, 15), label='TestData')
plt.legend()
plt.savefig('test_hist.png')
plt.show()
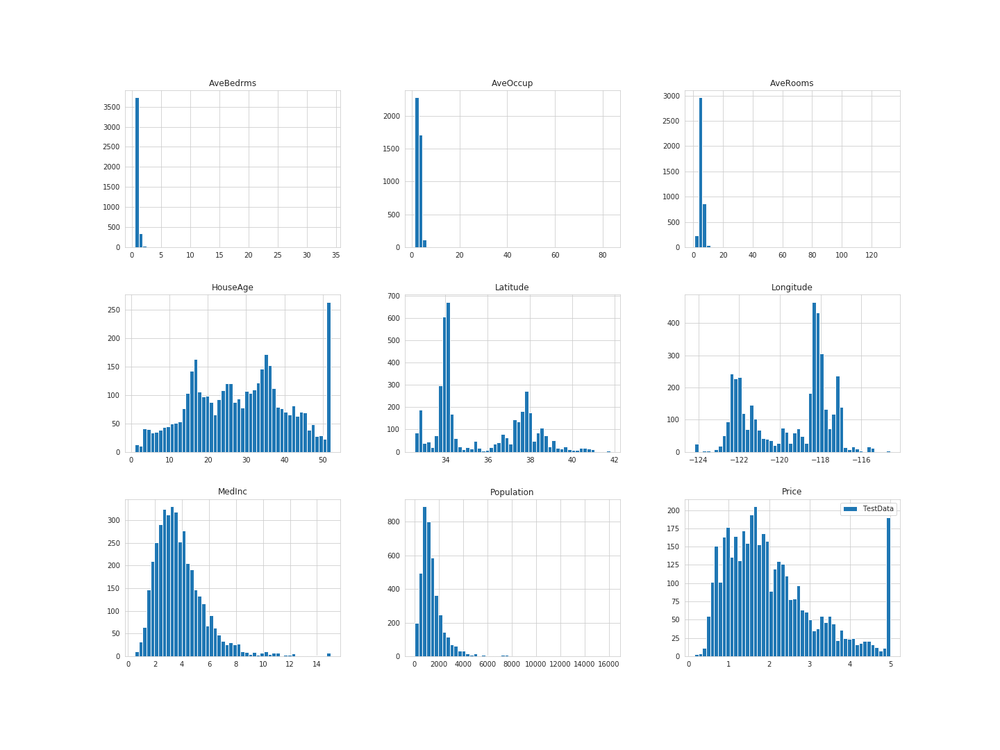
だいたい同じような分布となっています。
それでは訓練セットのみを使って分析していきます。
外れ値を取り除く¶
訓練セットを壊してしまわないようにコピーをしておきます。
# 実行
housing_sample = train_set.copy()
housing_sample.head()
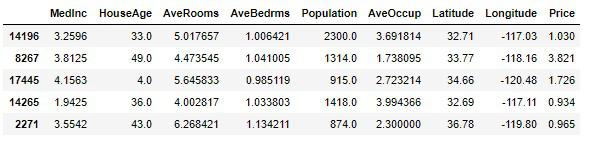
AveRooms、AveBedrms、AveOccupの値を見やすくするために四捨五入をし、小数点以下を切り捨てます。
# 実行
ave_columns = ['AveRooms', 'AveBedrms', 'AveOccup']
for col in ave_columns:
housing_sample[col] = np.round(housing_sample[col])
housing_sample.head()
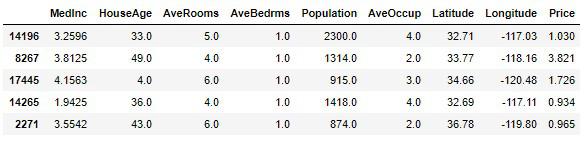
再び統計情報を確認してみます。
# 実行
housing_sample.describe()
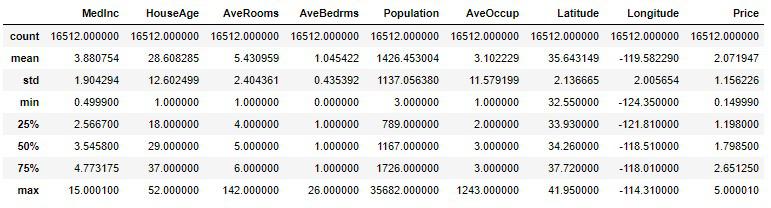
先ほど標準偏差や四分位範囲はそのデータの代表値と言いましたが、その代表値から大きく外れている値を見つけ出します。
ヒストグラムで描画すると、分布の広がり具合を確かめることができます。
# 実行
housing_sample.hist(bins=50, figsize=(15, 10))
plt.savefig('sample_hist.png')
plt.show()
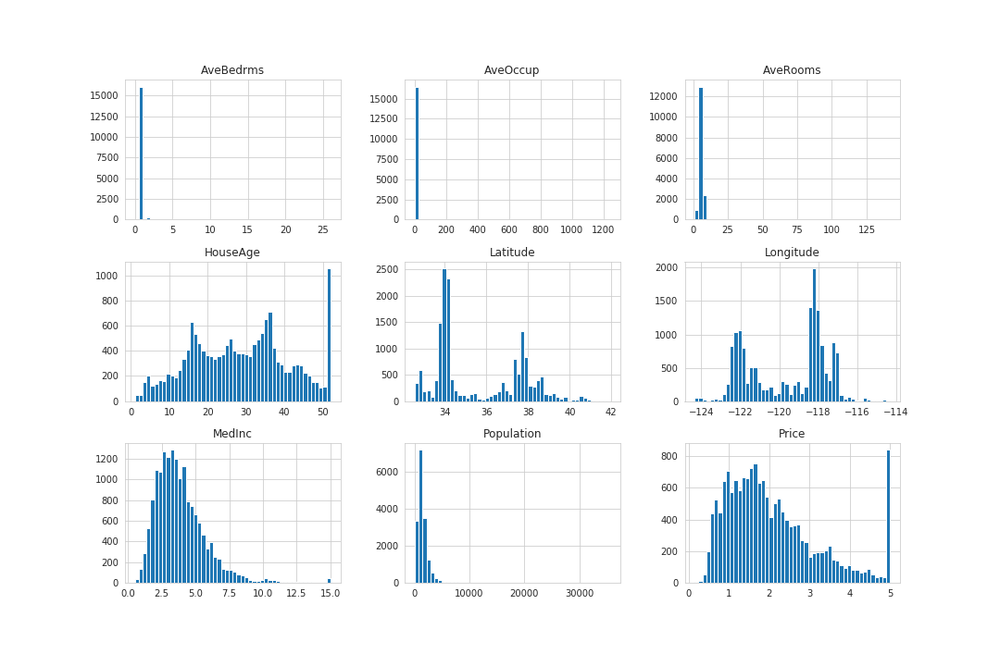
ヒストグラムは横軸に単位、縦軸に個数を棒によって可視化しています。
例えばPrice(住宅価格の中央値)の50万ドル辺りの数は1000以上のデータが存在すると言えます。
可視化をする際の引数で、bins=50やbins=100と指定することで、棒の太さ(単位)を調整することができます。
ポイントとしては、外れ値や他の値と比較して不自然な値を気にすることです。
外れ値とは、常識的でない値・他のまとまったデータと大きくかけ離れたような値です。AveBedrms、AveOccup、AveRoomsを見ると右側が大きく開いています。
不自然な値とはHouseAgeやPriceに表れている値です。最大値の単位が他の単位より不自然に多くなっていることがわかります。
# 実行
housing_sample[['HouseAge', 'Price']].hist(bins=50, figsize=(15, 6))
plt.savefig('house_price_hist.png')
plt.show()
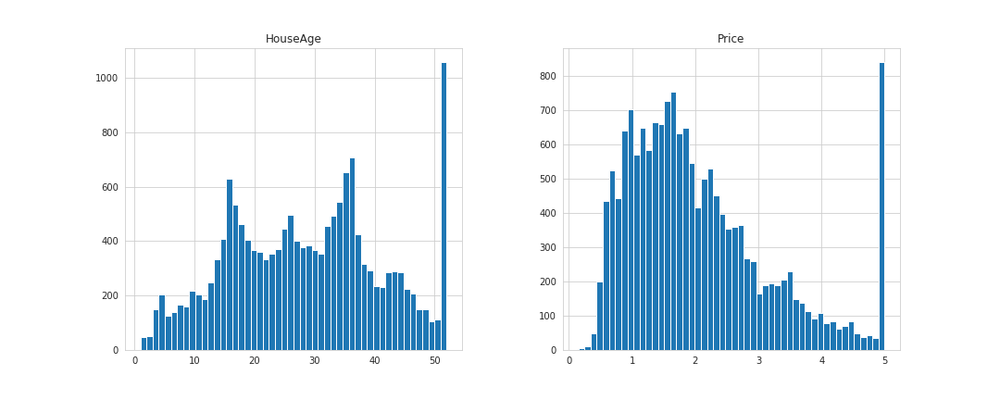
Price属性では20万ドル付近を境に値が下がっている傾向として見ることができますが、Price属性の常識を考えると50万ドルの合計値は不自然です。恐らく実際は50万ドル以上のデータがあって(60万ドルや80万ドルなど)、上限を50万ドルとしてまとめられていると思われます。
このようなデータをどう処理するかによって機械学習モデルの精度も変わってくるので、大事なポイントと言えます。
処理方法としては、それらの値を取り除いてしまうか、正確なデータへ変換するのが良いかと思います。
ここでは、前者の「取り除く」を選択して実行します。
# 実行
housing_sample[['HouseAge', 'Price']].describe()
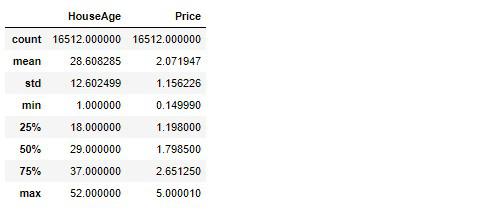
それぞれの最大値を取り除きます。
housing_sample = housing_sample[housing_sample['HouseAge'] < 52]
housing_sample = housing_sample[housing_sample['Price'] < 5]
もう一度可視化
# 実行
housing_sample[['HouseAge', 'Price']].hist(bins=50, figsize=(15, 6))
plt.savefig('house_price_del_hist.png')
plt.show()
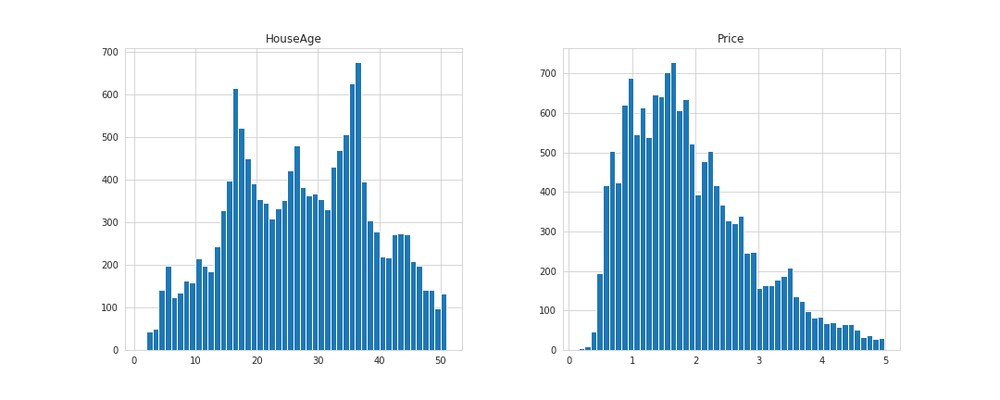
どれぐらいデータが減ってしまったか確認します。
# 実行
housing_sample.shape, train_set.shape
# 結果
((14832, 9), (16512, 9))
1700程のデータが削られてしまいました。データは貴重なので勿体ないですが精度を上げるためには致し方ないです。
次に外れ値を見ていきます。
# 実行
housing_sample.describe()
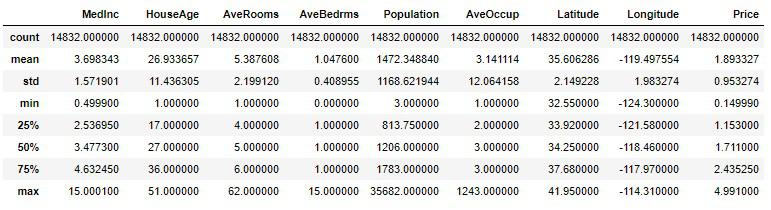
確認ですが、25%(第1四分位数)、50%(第2四分位数)、75%(第3四分位数)と区切られていて、50%が中央値、すなわちそのデータの小さい順からちょうど真ん中に当たる値です。
例えばMedIncの50%と75%を見ると、その差は約1万2千ドル程です。75%の値は50%とmax(最大値)の小さい順から真ん中に当たる値なので、75%とmaxの値は大きく離れていることが見受けられます。
従ってMedIncのmaxである15万ドルの値は外れ値なのではないか?と疑うことができます。
イメージを膨らませる為に1~10の値を30個使ってヒストグラムを表示してみます。
# 実行
number = np.arange(1, 11)
number_2 = np.arange(2, 10)
number_3 = np.arange(3, 9)
number_4 = np.arange(4, 8)
number_5 = np.arange(5, 7)
all_number = np.concatenate([number, number_2, number_3, number_4, number_5])
all_number
# 結果
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 2, 3, 4, 5, 6, 7, 8,
9, 3, 4, 5, 6, 7, 8, 4, 5, 6, 7, 5, 6])
# 実行
all_number = pd.DataFrame(all_number)
all_number.describe()

平均値と中央値が一致しています。ヒストグラムで表示するとベル型のような分布になることが見受けられます。
# 実行
all_number.hist(bins=50)
plt.savefig('number_hist.png')
plt.show()
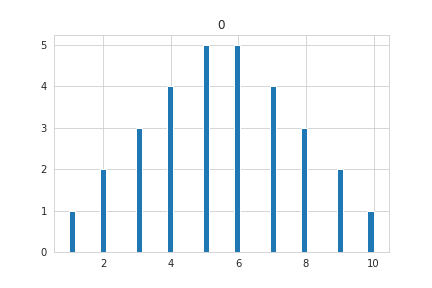
ヒストグラムに正規分布を重ねて描画してみます。
seabornにscipyモジュールのnormをフィッティングすると正規分布を描いてくれます。
# 実行
from scipy.stats import norm
sns.distplot(all_number, kde=False, fit=norm, fit_kws={'label': 'Normal Distribution'})
plt.legend()
plt.savefig('number_std.png')
plt.show()
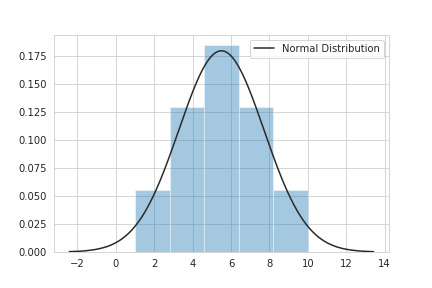
正規分布の頂点が平均値、平均値から±標準偏差(std)だと全体の68.3%、±標準偏差×2だと全体の95.4%、±標準偏差×3だと全体の99%の値が収まるという見方ができ、平均値と中央値が一致することで正規分布に従っていることになります。
逆に正規分布に従わない分布を表示してみます。
一番後ろのデータを大きい値に置き換えて正規分布を表示してみます。
# 実行
all_number_2 = all_number.copy()
all_number_2[-1:] = 50
all_number_2.describe()
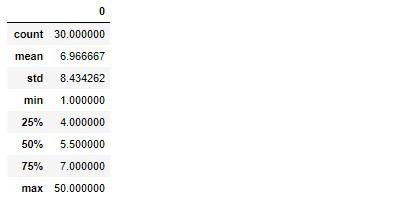
平均値と中央値にズレが生じました。では先ほどのグラフと見比べてみます。
# 実行
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13, 5))
sns.distplot(all_number, kde=False, fit=norm, fit_kws={'label': 'After'}, ax=ax1)
sns.distplot(all_number_2, kde=False, fit=norm, fit_kws={'label': 'Before'}, ax=ax2)
ax1.legend()
ax2.legend()
plt.savefig('After_&_Before.png')
plt.show()
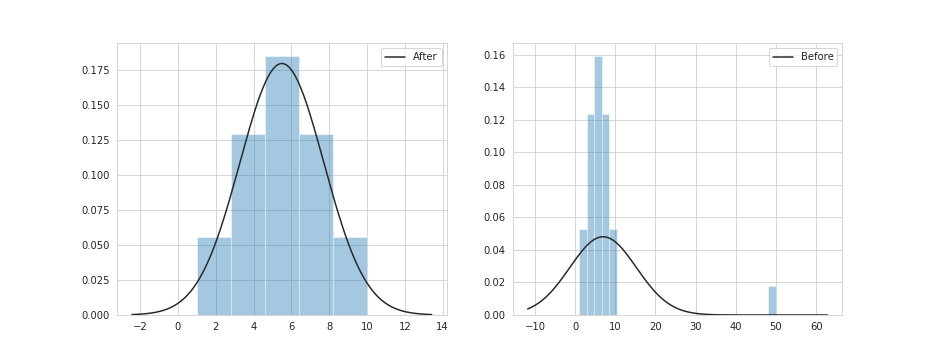
統計的観点から見るならば、このような外れ値は分散を広げ過ぎてしまい全体としての数値にとって相応しくないと言えます。
なのでヒストグラムを見ても分かる通り、MedInc、AveRooms、AveBedrms、Population、AveOccupの分布の広がりを少なくし(中央に分布させる)、左右対称な正規分布になるよう外れ値を取り除いていきます。
# 実行
housing_sample[['MedInc', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup']].hist(bins=50, figsize=(20, 15))
plt.savefig('outlier_1.png')
plt.show()
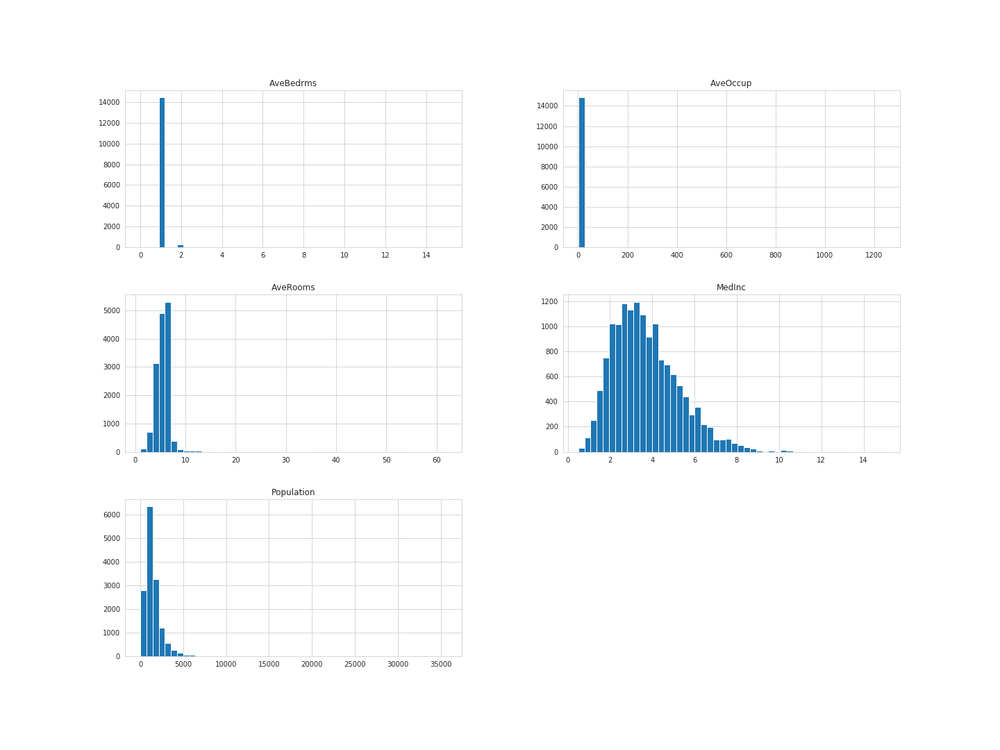
外れ値を取り除く際は、属性ずつ外れ値を探し出して取り除くには手間暇がかかってしまうので、全部まとめて取り除けるような処理を関数として書いていきます。
処理内容は四分位範囲を利用した除外や標準偏差を利用した除外など色々な除外方法があります。
今回は標準偏差を利用した外れ値の除外を行っていこうと思います。
標準偏差の2倍以上、すなわち95%範囲外の値を除外します。
試しにPopulationを使って試してみます。
# 実行
test_population = housing_sample['Population'].copy()
test_population.describe()
# 結果
count 14832.000000
mean 1472.348840
std 1168.621944
min 3.000000
25% 813.750000
50% 1206.000000
75% 1783.000000
max 35682.000000
Name: Population, dtype: float64
# 実行
sns.distplot(test_population, kde=False, fit=norm, fit_kws={'label': 'Normal Distribution'})
plt.legend()
plt.savefig('test_population.png')
plt.show()
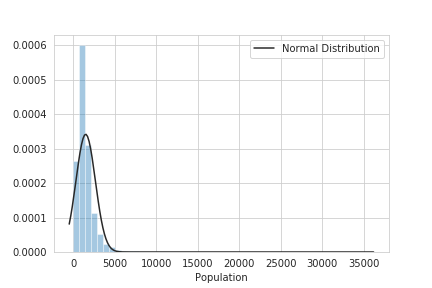
mean(平均値)から±std(標準偏差)の2倍が95%の範囲に収まるので、単純に計算すると以下の数値以上は除外されます。
# 実行
std_2 = test_population.std() * 2
std_p = test_population.mean() + std_2
std_m = test_population.mean() - std_2
print('平均値:{}'.format(test_population.mean()))
print('標準偏差×2:{}'.format(std_2))
print('最大値:{}'.format(std_p))
print('最小値:{}'.format(std_m))
print('\n')
print('実際の最大値:{}'.format(test_population.max()))
# 結果
平均値:1472.3488403451995
標準偏差×2:2337.24388857909
最大値:3809.592728924289
最小値:-864.8950482338903
実際の最大値:35682.0
ここでの結果は、平均から±標準偏差の2倍の数値は最大値が3809人で、最小値が-864人でした。
最大値以上、最小値以下の値は除外します。
では違う計算方法で、平均値から何倍離れているかを計算し、2倍以上の数値であれば除外するというコードを書いていきます。
# 実行
mean = test_population.mean()
std = test_population.std()
# 平均値で引いた値をnp.abs()で絶対値に置き換え標準偏差で割る
boder = np.abs(test_population - mean) / std
boder.head()
# 結果
14196 0.708228
8267 0.135500
17445 0.476928
14265 0.046507
2271 0.512012
Name: Population, dtype: float64
1以下の値は±標準偏差値の範囲で、2以下の値は±標準偏差値×2の範囲ということになります。
# 実行
test_population = test_population[(boder < 2)]
test_population.describe()
# 結果
count 14299.000000
mean 1318.964053
std 731.485954
min 3.000000
25% 799.000000
50% 1176.000000
75% 1696.500000
max 3806.000000
Name: Population, dtype: float64
平均値と中央値に差はありますが、とりあえず良しとしてグラフを表示してみます。
# 実行
sns.distplot(test_population, kde=False, fit=norm, fit_kws={'label': 'Normal Distribution'})
plt.legend()
plt.savefig('test_population_outlier.png')
plt.show()
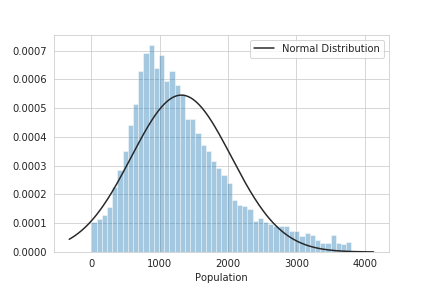
だいぶ中央にまとまった分布となりました。
この方法を使って、for文で他の属性も外れ値を取り除いていきます。後ほど関数として定義します。
# 実行
columns = housing_sample[['MedInc', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup']].columns
for col in columns:
mean = housing_sample[col].mean()
std = housing_sample[col].std()
boder = np.abs(housing_sample[col] - mean) / std
housing_sample = housing_sample[(boder < 2)]
housing_sample.describe()
# 実行
housing_sample[['MedInc', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup']].hist(bins=50, figsize=(20, 15))
plt.savefig('all_outlier.png')
plt.show()
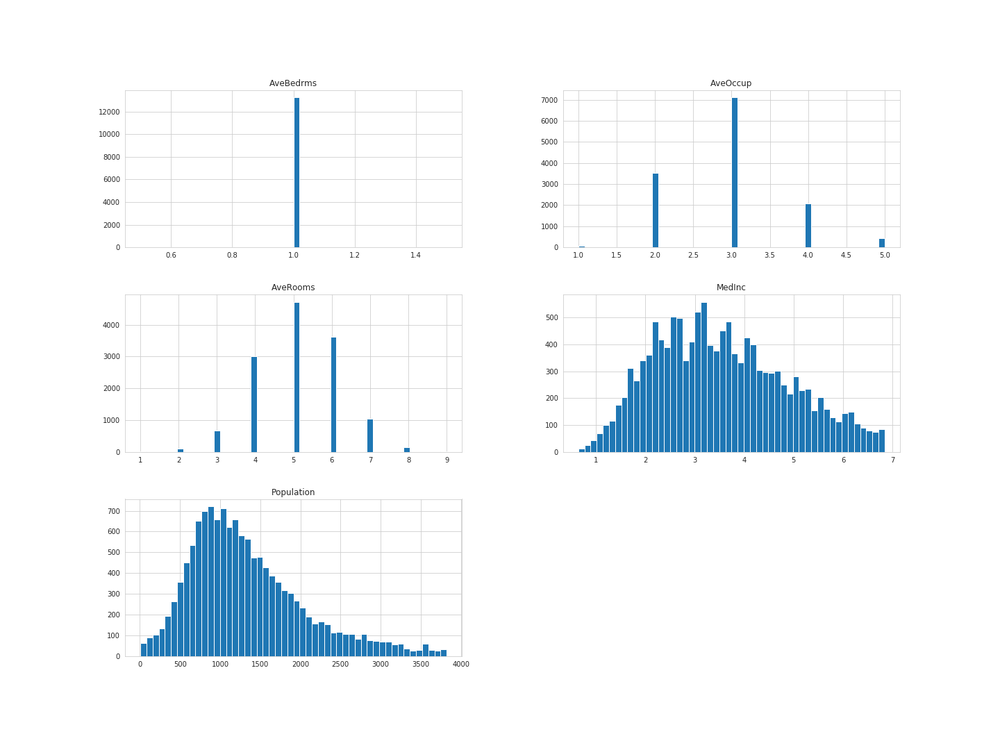
だいぶまとまりのある分布に変換できたかと思います。
AveBedrmsが特徴量としての要素を無くしてしまいましたが、後ほど特徴量抽出に使うので取っておきます。
特徴量エンジニアリング¶
ここからは、特徴量を新たに作って行こうと思います。
現在8つの特徴量が存在していますが、そのいずれかの特徴量を組み合わせたり、外部の情報を元に得られた相関のありそうな特徴量を加えることで、機械学習の精度を良くすることができる場合があります。
相関(Correlation)というのは、2つのデータ間にある影響度合いのことです。
例えば住宅価格と収入の相関をイメージすると、住宅価格が上がると収入も上がるという傾向があります。互いのデータ間がプラスに働くと正の相関、片方のデータがマイナスに働くと負の相関であるといいます。プラスにもマイナスにも働かない相関は無相関といいます。
pandasのcorr()を使って相関係数を見てみます。相関係数は-1から1の値を表す各属性間に対する係数です。
Price属性に対する各属性の相関係数を表示します。
# 実行
housing_sample.corr()['Price'].sort_values()
# 結果
AveOccup -0.258252
Latitude -0.177601
Longitude -0.018615
Population 0.010828
HouseAge 0.048966
AveRooms 0.186584
MedInc 0.611532
Price 1.000000
AveBedrms NaN
Name: Price, dtype: float64
Price(住宅価格の中央値)が上がることによって、他の属性がプラスに変化しているのか?、マイナスに変化しているのか?、を確認することができます。プラスが正、マイナスが負として0に近ければその属性はPriceに対して影響を及ぼさないことがわかります。
Priceに対して一番正に働いている属性はMedInc、一番負に働いている属性はAveOccupという結果でした。
AveBedrmsのデータは全て1となったので、有っても無くても変わらない、つまり無相関だということが分かります。
ではPriceに対するMedIncとAveOccupの相関を可視化してみます。散布図をプロットすることによって相関図を表示できます。
まずはSeabornを使ってPriceとMedIncの関係性を可視化します。
# 実行
sns.regplot('Price', 'MedInc', data=housing_sample, scatter_kws={'alpha': 0.4}, line_kws={'color': 'red'})
plt.savefig('med_correlation.png')
plt.show()
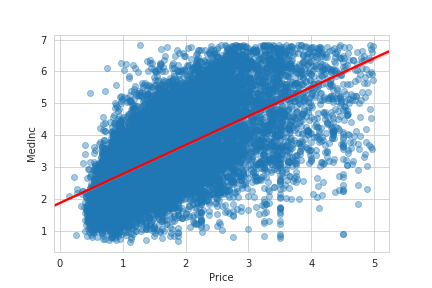
regplot()によって回帰直線を引いてくれます。右肩上がりになっている場合は正に強い相関があると伺えます。
ではAveOccupの相関図を可視化してみます。
# 実行
sns.regplot('Price', 'AveOccup', data=housing_sample, scatter_kws={'alpha': 0.4}, line_kws={'color': 'red'})
plt.savefig('occ_correlation.png')
plt.show()
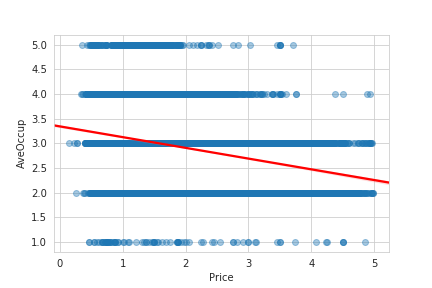
今度は右肩下がり、つまり負に強い相関が伺えます。住宅価格が上がる一方、平均世帯数の数は減る傾向にあります。
ついでに、経度と緯度の属性があるので、散布図を使い地理情報を可視化して住宅価格の特徴を見てみます。
# 実行
housing_sample.plot(kind='scatter', x='Longitude', y='Latitude', alpha=0.4,
figsize=(10, 7),
c='Price', cmap=plt.get_cmap('jet'), colorbar=True)
plt.savefig('longitude_latitude_is_price.png')
plt.show()
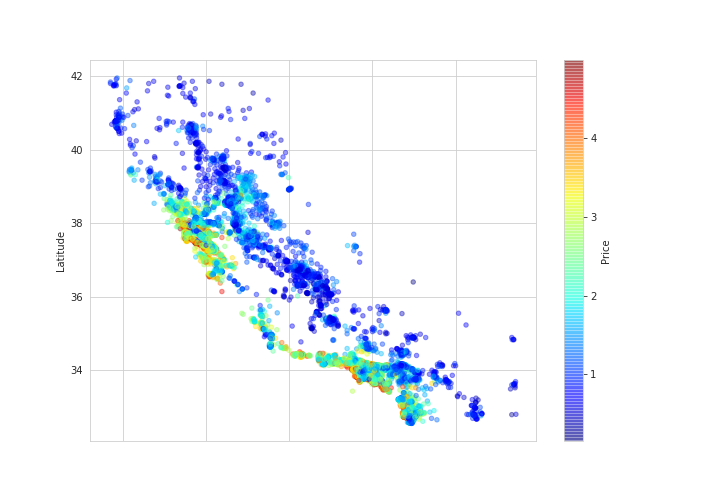
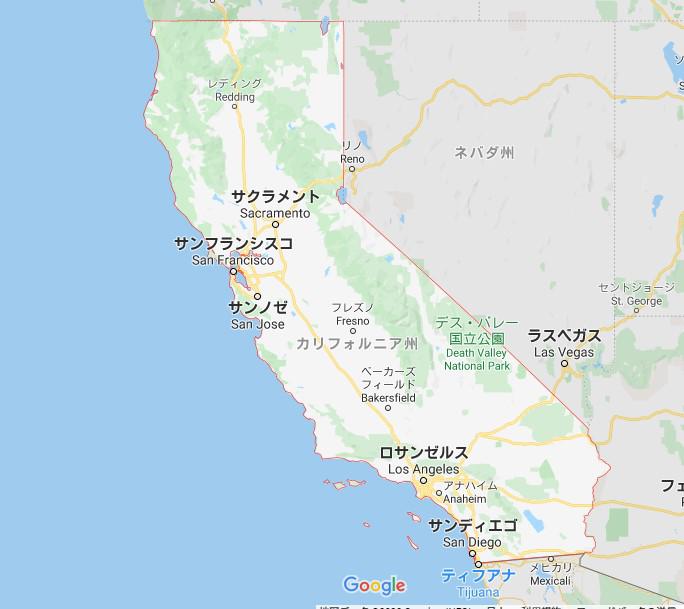
海に近いほど、住宅価格が高くなる傾向があるようです。
では経度と緯度を取り除いた全体の相関関係をSeabornを使って可視化してみます。
# 実行
plt.figure(figsize=(15, 13))
sns.pairplot(housing_sample.drop(['Latitude', 'Longitude'], axis=1))
plt.savefig('all_correlation.png')
plt.show()
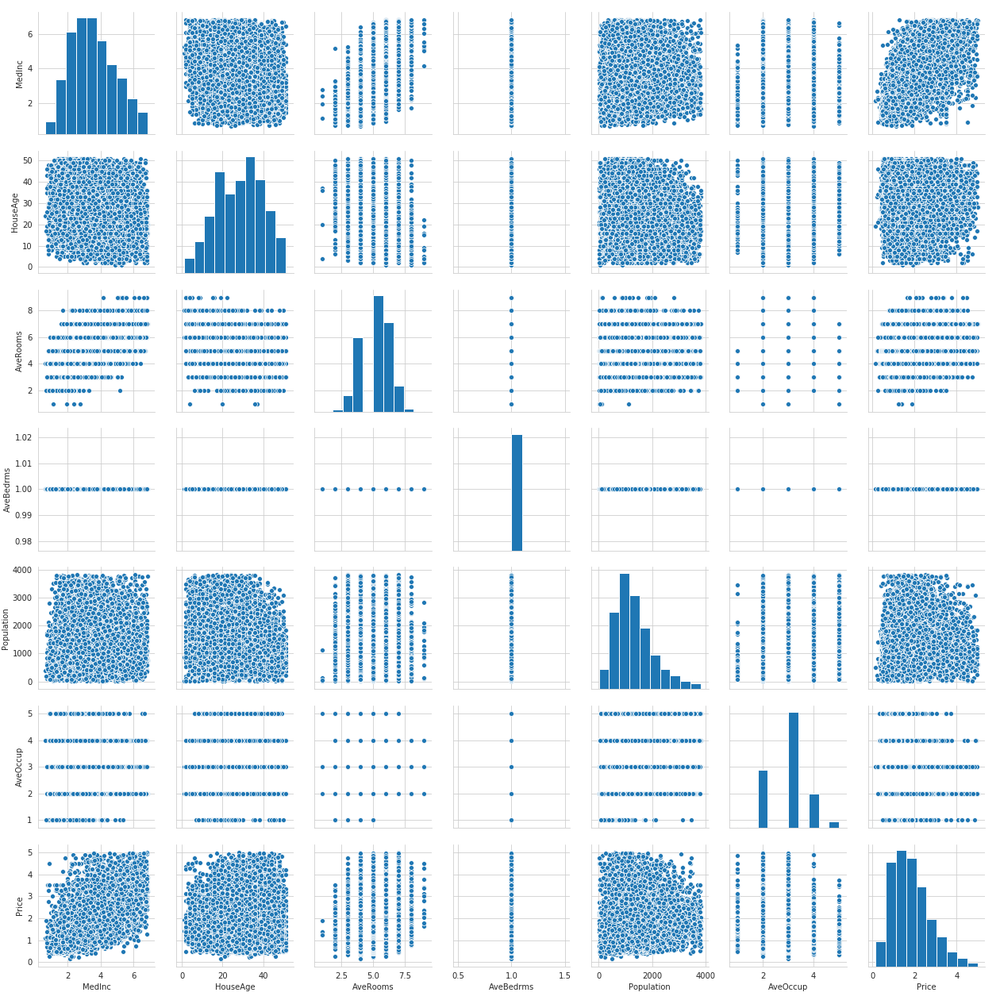
ここまで相関について見ていきましたが、相関関係がありそうな特徴量を新たに加えることで結果も大きく変わってくる場合があります。
正や負になる相関は目的変数に対して何等かの因果があると言えるので、機械学習モデルに良い影響を与えてくれると考えられます。
そのような特徴量を見つけることを、特徴量エンジニアリングや特徴量抽出と言います。
ここでは簡単になりますが、ある属性間の割合を新たな特徴量として加え、またある属性からカテゴリカルなデータを抽出し、ダミー変数として新たな特徴量として加えていきたいと思います。
では最初に、AveRoomsに対してAveBedrmsの数を比較します。
部屋数に対して寝室数は何%占めているのか?、もちろん寝室数は外れ値の処理時に全て1の値になってしまったので余り意味はありませんが練習として実装していきます。
# 実行
housing_sample['Bedrms_per_Rooms'] = housing_sample['AveBedrms'] / housing_sample['AveRooms']
housing_sample.head()
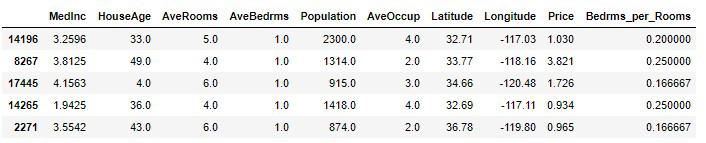
Price属性に対する各相関係数を確認してみます。
# 実行
housing_sample.corr()['Price'].sort_values()
# 結果
AveOccup -0.258252
Latitude -0.177601
Bedrms_per_Rooms -0.127661
Longitude -0.018615
Population 0.010828
HouseAge 0.048966
AveRooms 0.186584
MedInc 0.611532
Price 1.000000
AveBedrms NaN
Name: Price, dtype: float64
新しい特徴量のBedrms_per_RoomsではPriceに対して負の相関であることが分かります。AveBedrmsの代わりに機械学習モデルに適用してみましょう。
PriceとBedroms_per_Roomsの相関を可視化してみます。
# 実行
sns.regplot('Price', 'Bedrms_per_Rooms', data=housing_sample, scatter_kws={'alpha': 0.4}, line_kws={'color': 'red'})
plt.savefig('bed_per_room_correlation.png')
plt.show()
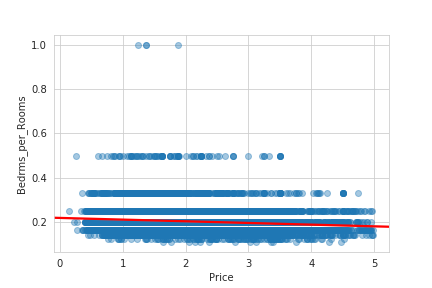
若干ですが右肩下がりとなっているのが分かると思います。
次にPopulation(区域内の人口)属性を使って、ある特定の人口数に収まっているか、そうでないかというカテゴリー属性を抽出していきたいと思います。
人口はどの辺りに多く集まっているかを、地理情報を散布図で可視化してみます。
# 実行
housing_sample.plot(kind='scatter', x='Longitude', y='Latitude', alpha=0.4,
figsize=(10, 7),
c='Population', cmap=plt.get_cmap('jet'), colorbar=True)
plt.savefig('longitude_latitude_is_population.png')
plt.show()
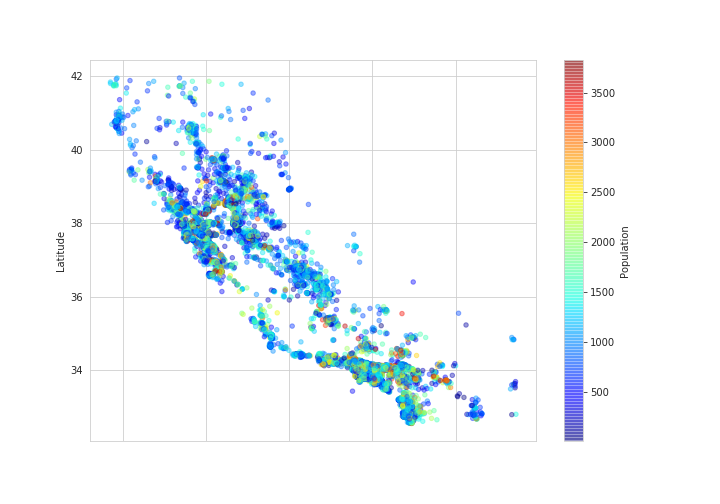
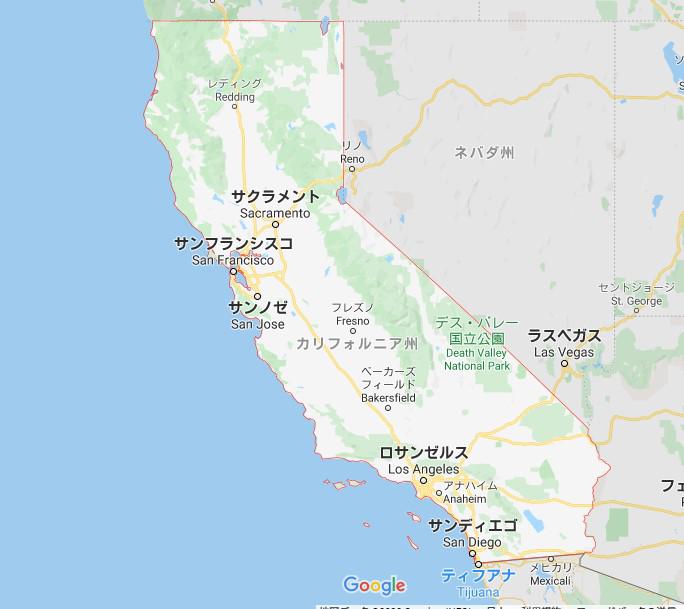
地図と比べて見ると、何となくサンフランシスコ、サクラメント、ロサンゼルス周辺の区域の人口が比較的に多い気がします。
ではPopulationを使い、区域内の人口は少ない・普通・多いというカテゴリーを作って行きます。指標はデータセットの詳細説明にあった、ほとんどの区域の人口は600人から3000人ということから、この範囲に収まる人口は普通、この範囲の最小値以下は少ない、最大値以上は多いとして新たな属性を加えていきます。
1つ1つのデータを比較できるように関数を作っておきます。
def category(df):
if df < 600:
# 少ない
return 'few'
elif df > 3000:
# 多い
return 'many'
else:
# 普通
return 'usually'
pandasのapply()を使って関数を適用させます。
# 実行
housing_sample['Population_Feature'] = housing_sample['Population'].apply(category)
housing_sample.head(10)
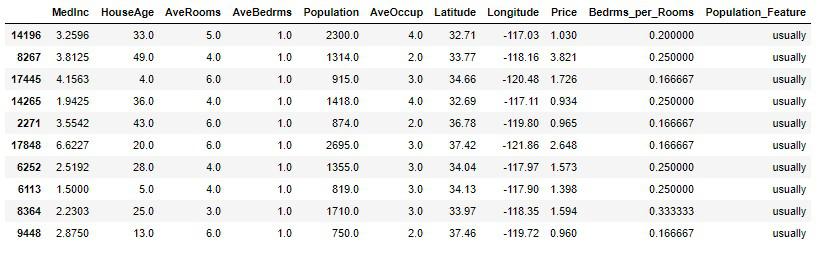
このPopulation_Featureに対し、ダミー変数を適用していきます。
ダミー変数とは、数値でないデータを0か1の数値に置き換えて、そのデータに付加を与えてくれます。
文字列型のデータは機械学習に適用できないので、ダミー変数に変換することは有効な手法として使われます。
pandasのpd.dummies()によってダミー変数を作ることができます。
# 実行
feature_dummies = pd.get_dummies(housing_sample['Population_Feature'])
feature_dummies.head()
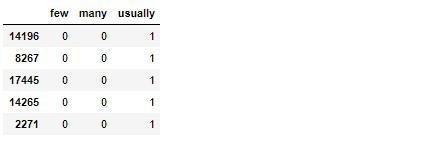
ダミー変数化にする際は多重共線性という現象に考慮する必要があります。多重共線性は説明変数内で高い相関関係がある場合に起こる現象で、精度を落としてしまうと言われています。
例えばfewが1の場合、他のカテゴリーmanyとusuallyは0になります。fewが0の場合は他のどれかが必ず1となるような高い相関をもった属性は取り除くことにより解消されると言います。
そこで、pd.dummies()の引数に、drop_first=Trueとすることで最初の属性を取り除いたダミー変数を抽出してくれます。
# 実行
feature_dummies = pd.get_dummies(housing_sample['Population_Feature'], drop_first=True)
feature_dummies.head()

では抽出したダミー変数を元のデータと結合します。
# 実行
housing_sample = pd.concat([housing_sample, feature_dummies], axis=1)
housing_sample.head()

相関係数を見てみます。
# 実行
housing_sample.corr()['Price'].sort_values()
# 結果
AveOccup -0.258252
Latitude -0.177601
Bedrms_per_Rooms -0.127661
Longitude -0.018615
usually -0.002524
many 0.003439
Population 0.010828
HouseAge 0.048966
AveRooms 0.186584
MedInc 0.611532
Price 1.000000
AveBedrms NaN
Name: Price, dtype: float64
ダミー変数の相関は低いですが、このまま機械学習に適用してみましょう。
これで一通りの前処理を終えました。
各処理ごとに説明を行ってきましたが、まだまだ十分ではないと自分では思っています。説明不足であったり、理論的におかしい、といった部分もあるかもしれません。
なので、あくまで参考程度に留めておき、色々なサイトを見て学び、各自の答えを見つけ出してください。
では次に、スケーリングについて見ていきます。
特徴量スケーリング(標準化)¶
データをクリーニングしたあと、機械学習へ適用させる前にスケーリングを行う場合があります。
スケーリングとは標準化のことで、各属性の平均を0、分散を1まで幅を揃えて外れ値への影響を少なくさせます。
標準化をすることによって、それぞれ異なった属性の平均や標準偏差(分散)を標準正規分布に従う指標に置き換えることができます。
MedIncを使って少し説明しますが、そもそも標準偏差を求めるには、(データ-データの平均値)の二乗をし、求められた各データの合計値をデータの数で割ることで分散を求めることができます。
分散に平方根(ルート)をとると標準偏差になります。
# 実行
housing_Med = housing_sample['MedInc'].copy()
# ((データ-平均値)の二乗)の合計値÷データ数
dispersion = ((housing_Med - housing_Med.mean()) * (housing_Med - housing_Med.mean())).sum() / len(housing_Med)
# 上と同じ
# dispersion = ((housing_Med - housing_Med.mean()) ** 2).sum() / len(housing_Med)
# np.sqrtで平方根をとる
standard_deviation = np.sqrt(dispersion)
print('手計算の標準偏差:{}'.format(standard_deviation))
print('pandasのstd:{}'.format(housing_Med.std()))
# 結果
手計算の標準偏差:1.3385871894505794
pandasのstd:1.3386376745508048
平均と標準偏差が分かれば、標準化を行うことができる。
# 実行
standardization_1 = (housing_Med - housing_Med.mean()) / housing_Med.std()
# np.roundで四捨五入し整数に直す
print('平均:{0}、分散:{1}'.format(np.round(standardization_1.mean()), np.round(standardization_1.std())))
# 結果
平均:-0.0、分散:1.0
Scipyモジュールのzscoreを使うと簡単に標準化することができます。
# 実行
from scipy.stats import zscore
standardization_2 = zscore(housing_Med)
print('平均:{0}、分散:{1}'.format(np.round(standardization_2.mean()), np.round(standardization_2.std())))
# 結果
平均:-0.0、分散:1.0
scikit-learnで標準化を行う場合はStandardScalerを使用します。
初期化を行った後、scaler.fit()で平均と標準を計算します。そしてscaler.transform()で計算されたデータを元にスケーリング(標準化)を実行します。
計算と実行をまとめて行う場合は、scaler.fit_transformt()を実行します。
# 実行
from sklearn.preprocessing import StandardScaler
# 初期化
scaler = StandardScaler()
# pandasのSeriesだと1次元配列になっているためnumpyのreshape()で2次元配列にする
standardization_3 = scaler.fit_transform(np.array(housing_Med).reshape(-1, 1))
# もしくわ
# scaler.fit(np.array(housing_Med).reshape(-1, 1))
# standardization_3 = scaler.transform(np.array(housing_Med).reshape(-1, 1))
print('平均:{0}、分散:{1}'.format(np.round(standardization_3.mean()), np.round(standardization_3.std())))
# 結果
平均:-0.0、分散:1.0
ヒストグラムを表示してみます。
値はスケーリングされましたが、重複された値の数は変わっていません。
# 実行
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13, 5))
sns.distplot(housing_Med, kde=False, label='Before', ax=ax1)
sns.distplot(standardization_3, kde=False, label='After', ax=ax2)
ax1.legend()
ax2.legend()
plt.savefig('Before_After.png')
plt.show()
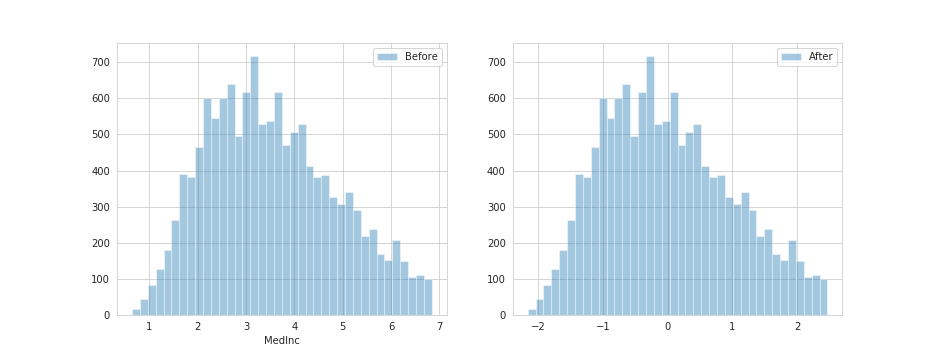
このように、各属性を平均0、分散1に揃えることによって機械学習モデルでは正しく学習を行うことができます。
StandardScalerではinverse_transformを使って元の値に戻すことができます。
# 実行
scaler.inverse_transform(housing_Med)
# 結果
array([[3.2596],
[3.8125],
[4.1563],
...,
[3.05 ],
[2.9344],
[5.7192]])
前処理用のカスタム変換器¶
前処理で行った処理を一括で行えるように、関数を1つのカスタム変換器としてまとめます。
def round_number(df):
"""
指定された属性の値を四捨五入し整数に置き換える
"""
ave_columns = ['AveRooms', 'AveBedrms', 'AveOccup']
for col in ave_columns:
df[col] = np.round(df[col])
return df
def std_exclude(df):
"""
標準偏差の2倍以上の値は取り除く
"""
columns = df[['MedInc', 'AveRooms', 'Population', 'AveOccup']].columns
for col in columns:
mean = df[col].mean()
std = df[col].std()
boder = np.abs(df[col] - mean) / std
df = df[(boder < 2)]
return df
def category(df):
"""
その区域の人口は、少ない(few)か、普通(usually)か、多い(many)か。
大体のの区域では600人から3000人ということから、この範囲を指標とする。
"""
if df < 600:
return 'few'
elif df > 3000:
return 'many'
else:
return 'usually'
""" 上3つの関数をまとめたカスタム変換器"""
def custom_conversion(dataframe):
df = dataframe.copy()
df = round_number(df)
# サンプルの調査ミスとして取り除く
df = df[df['HouseAge'] < 52]
# サンプルの調査ミスとして取り除く
df = df[df['Price'] < 5]
df = std_exclude(df)
# 平均部屋数に対して平均寝室数を比較する
df['Bedrms_per_Rooms'] = df['AveBedrms'] / df['AveRooms']
df['Population_Feature'] = df['Population'].apply(category)
# カテゴリー属性をダミー変数化する
feature_dummies = pd.get_dummies(df['Population_Feature'], drop_first=True)
df = pd.concat([df, feature_dummies], axis=1)
# Xを説明変数、yを目的変数に代入しておく
X = df.drop(['AveBedrms', 'Price', 'Population_Feature'], axis=1)
y = df['Price']
return X, y
機械学習へ適用¶
では変換器を使ってデータを前処理しましょう。
X, y = custom_conversion(train_set)
# 実行
X.head()
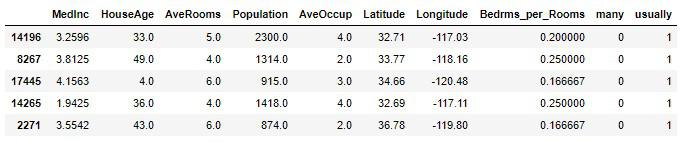
# 実行
y.head()
# 結果
14196 1.030
8267 3.821
17445 1.726
14265 0.934
2271 0.965
Name: Price, dtype: float64
説明変数に対し、スケーリングを行います。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_s = scaler.fit_transform(X)
# もしくわ
# scaler.fit(X)
# X_s = scaler.transform(X)
前回の第1回目では、検証セットにまで分割を行いましたが今回は全て訓練データとして適用させます。
これで機械学習で訓練を行う準備が整いました。
機械学習モデルは前回同様、正規方程式からなる線形回帰モデルで行います。同じモデルを使用することで、前処理無しと前処理有りでどれくらいの差が生まれるかが確認できます。
ではスケーリングされた説明変数X_sを適用させます。
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_s, y)
scikit-learnのmean_squared_error()で平均二乗誤差(MSE)を求め、求められた平均二乗誤差に平方根をとり(RMSE)実際の単位を算出します。
# 実行
from sklearn.metrics import mean_squared_error
lin_train_pred = lin_reg.predict(X_s)
lin_train_mse = mean_squared_error(y, lin_train_pred)
lin_train_rmse = np.sqrt(lin_train_mse)
print('訓練データの誤差:{:2f}'.format(lin_train_rmse))
# 結果
訓練データの誤差:0.575462
第1回目の訓練セットと検証セット共に誤差0.72(7万2千ドル)程でしたので、約0.15(1万5千ドル)縮めることができました。
誤差の値は小さければ小さいほど精度が良いということなので、前回よりは正しく学習を行い精度を上げることができました。
ラベルと予測値の残差を可視化してみます。
# 実行
plt.figure(figsize=(10, 8))
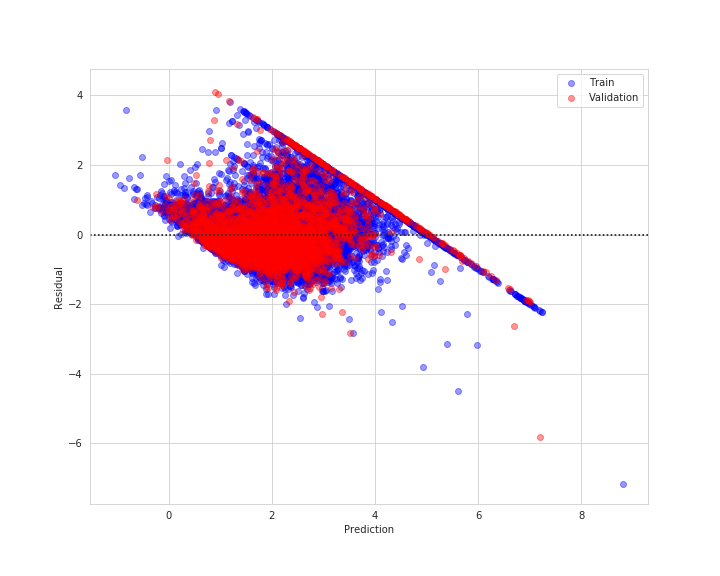
sns.residplot(lin_train_pred, y - lin_train_pred, scatter_kws={'alpha': 0.4})
plt.xlabel('Prediction(X)')
plt.ylabel('Residual(y)')
plt.savefig('resid_train.png')
plt.show()
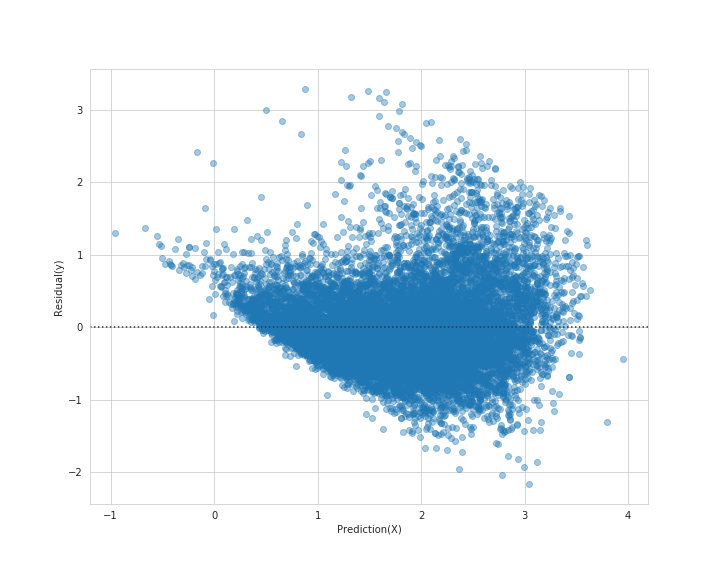
前回の訓練セット検証セットの残差より、散らばり具合も縮小されています。
ではテストセットでの評価を行います。
訓練セット同様テストセットにもカスタム変換器に渡し、前処理後、説明変数と目的変数に分割しスケーリングをします。
※テストセットでスケーリングを行う際は、scaler.fit_transform()ではなく、scaler.transform()を使い訓練セットで求められた計算を元にスケーリングします。
# 実行
X_test, y_test = custom_conversion(test_set)
# スケーリング
X_test = scaler.transform(X_test)
# 評価を行う
best_model_pred = lin_reg.predict(X_test)
best_model_mse = mean_squared_error(y_test, best_model_pred)
best_model_rmse = np.sqrt(best_model_mse)
print('テストデータの誤差:{:2f}'.format(best_model_rmse))
# 結果
テストデータの誤差:0.587216
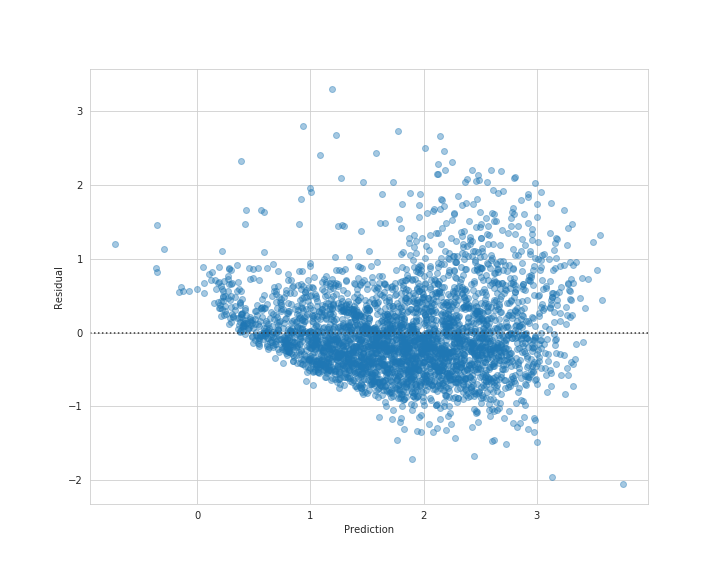
訓練セットより少し精度は落ちましたが、上手く汎化されているかと思います。
# 実行
plt.figure(figsize=(10, 8))
sns.residplot(best_model_pred, y_test - best_model_pred, scatter_kws={'alpha': 0.4})
plt.xlabel('Prediction')
plt.ylabel('Residual')
plt.savefig('resid_test.png')
plt.show()
それではKaggleでもお馴染みの提出用に予測結果を保存しておきます。
submission = pd.DataFrame({
'Price': y_test,
'Prediction': np.round(best_model_pred, 3)
})
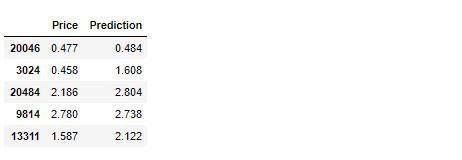
データを保存します。
submission.to_csv('housing_submission_2.csv')
課題¶
今回はデータのクリーニング(前処理)を中心に実装していきました。
欠損値の除外・穴埋め、外れ値の検出方法、特徴量抽出などの処理はデータの数によって計算されるので、各処理内容の順番が前後すれば結果も変わってくる場合があります。
前処理にしてもまだまだ課題はありますが、ここで行った内容はあくまで参考程度に留め、様々な人の色々な処理方法を学び、独自のテクニックを磨いてください。
そして次の課題は、機械学習モデルについてです。
- 単純な機械学習モデルを使用したので、複雑なモデルを試してみる。
- 幾つかのハイパーパラメータを設定し、精度を再確認
- 過学習対策
第1回目、第2回目と線形回帰モデルのみを試してきたので、次回の第3回目では他の機械学習モデルを使い、最も精度の良いモデルを選び出してからテストセットを評価してみようと思います。
【第3回カリフォルニア住宅価格の予測】最良の機械学習モデルを選び評価を行う
それでは以上となります。
最後までご覧いただきありがとうございました。
