【第3回カリフォルニア住宅価格の予測】最良の機械学習モデルを選び評価を行う
投稿日 2020年4月21日 >> 更新日 2024年7月9日
※誤ってscaler.fit_transform(X_test)とテストセットに対して平均と標準の計算をし直してしまったため(正確にはscaler.transform(X_test))、依然と結果は大きく変わりましたので、後半の内容を変更させて頂きました。
今回はカリフォルニア住宅価格の予測第3回ということで、最良の機械学習モデルを選び出し未知のデータに対し評価を行っていこうと思います。
少し振り返りますが、第1回目では読み込んだデータに前処理を行わず、最も単純な機械学習モデルで訓練し評価を行いました。
結果は余り良いとは言えませんでしたが、残差プロットを見てみると外れ値や一定に分布されている特徴が見受けられました。
【第1回カリフォルニア住宅価格の予測】前処理無しで精度を確認
そして第1回目の課題として、第2回目ではデータの前処理(クリーニング)を主に実装し、同じく単純な機械学習モデルでの訓練を行った結果、第1回目の予測値と正解ラベルの誤差を0.15(1万5千ドル)ほど縮めることができました。
【第2回カリフォルニア住宅価格の予測】特徴量エンジニアリング&データクリーニング(データクレンジング)
前回までは機械学習モデルが正しく学習を行えるようデータを整えてきましたが、まだ単純なモデルである線形回帰モデルでしか評価を行っていません。
今回の課題は、幾つかの機械学習モデルで訓練を行い、過小適合や過学習という問題も含め最良の機械学習モデルを選び出し未知のデータに対して評価を行っていこうと思います。
実行環境&使用ライブラリ¶
| 実行環境 |
|---|
| Windows Subsystem for Linux |
| Python 3.6.9 |
| pip 9.0.1 |
| Jupyter notebook |
| 使用ライブラリ | ライセンス |
|---|---|
| numpy==1.16.4 | OSI Approved (new BSD) |
| pandas==0.25.0 | BSD |
| matplotlib==3.1.1 | PSF |
| seaborn==0.9.0 | BSD |
| scikit-learn==0.21.3 | OSI Approved (new BSD) |
データの準備¶
まずは必要なデータを読み込んで、訓練セットとテストセットに分割しておきます。
※必要なライブラリもインポートしておきます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
説明変数X、目的変数(正解ラベル)yに格納。
housing = fetch_california_housing()
X = pd.DataFrame(housing.data, columns=housing.feature_names)
y = pd.DataFrame(housing.target, columns=['Price'])
訓練セットとテストセットに分割。
# 実行
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
X_train.shape, X_test.shape
# 結果
((16512, 8), (4128, 8))
ここではデータセットの20%をテストセットとして分割しました。
では説明変数と目的変数をそれぞれpandasのデータフレームに格納します。
train_set = pd.concat([X_train, y_train], axis=1)
test_set = pd.concat([X_test, y_test], axis=1)
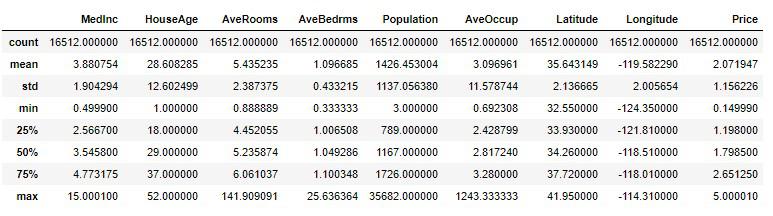
統計情報をザックリと確認しておきます。
# 実行
train_set.describe()
テストセットの統計情報。
# 実行
test_set.describe()
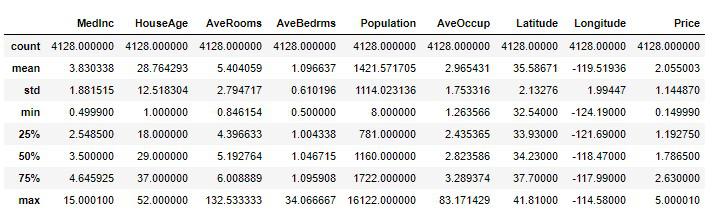
テストセットは未知のデータとするので、最後の評価用にとっておき、訓練セットを前処理します。
前処理は第2回で行った処理方法で実践するので、その際に作ったカスタム変換器を使用して処理を実装します。
カスタム変換器
def round_number(df):
"""
指定された属性の値を四捨五入し整数に置き換える
"""
ave_columns = ['AveRooms', 'AveBedrms', 'AveOccup']
for col in ave_columns:
df[col] = np.round(df[col])
return df
def std_exclude(df):
"""
標準偏差の2倍以上の値は取り除く
"""
columns = df[['MedInc', 'AveRooms', 'Population', 'AveOccup']].columns
for col in columns:
mean = df[col].mean()
std = df[col].std()
boder = np.abs(df[col] - mean) / std
df = df[(boder < 2)]
return df
def category(df):
"""
その区域の人口は、少ない(few)か、普通(usually)か、多い(many)か。
大体のの区域では600人から3000人ということから、この範囲を指標とする。
"""
if df < 600:
return 'few'
elif df > 3000:
return 'many'
else:
return 'usually'
""" 上3つの関数をまとめたカスタム変換器"""
def custom_conversion(dataframe):
df = dataframe.copy()
df = round_number(df)
# サンプルの調査ミスとして取り除く
df = df[df['HouseAge'] < 52]
# サンプルの調査ミスとして取り除く
df = df[df['Price'] < 5]
df = std_exclude(df)
# 平均部屋数に対して平均寝室数を比較する
df['Bedrms_per_Rooms'] = df['AveBedrms'] / df['AveRooms']
df['Population_Feature'] = df['Population'].apply(category)
# カテゴリー属性をダミー変数化する
feature_dummies = pd.get_dummies(df['Population_Feature'], drop_first=True)
df = pd.concat([df, feature_dummies], axis=1)
# Xを説明変数、yを目的変数に代入しておく
X = df.drop(['AveBedrms', 'Price', 'Population_Feature'], axis=1)
y = df['Price']
return X, y
この変換器は前処理をされたあと、戻り値として目的変数と説明変数に分割されるので、Xとyの変数を準備します。
X, y = custom_conversion(train_set)
前処理後の統計情報を確認してみます。
# 実行
X.describe()
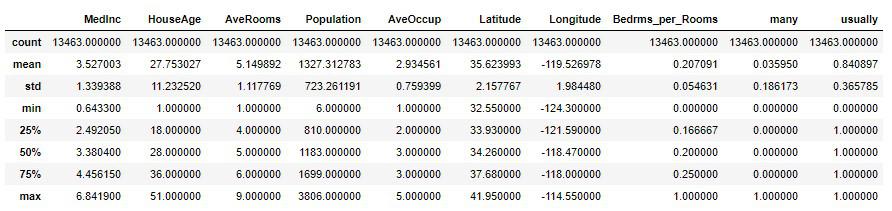
平均値と中央値(50%)の差が割と近いので、大きく外れたような値は取り除けているようです。
では説明変数に対しスケーリングを行ったら準備完了です。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_s = scaler.fit_transform(X)
複雑な機械学習モデルを使って訓練を行う¶
それではさっそく、幾つかの複雑な機械学習モデルを訓練させてみて、それぞれの結果で最も最良なモデルを選び出していきたいと思います。
前回まで行ってきた線形回帰モデルでは、与えられるデータが単純な直線を引けるような前提のもと訓練を行っていました。
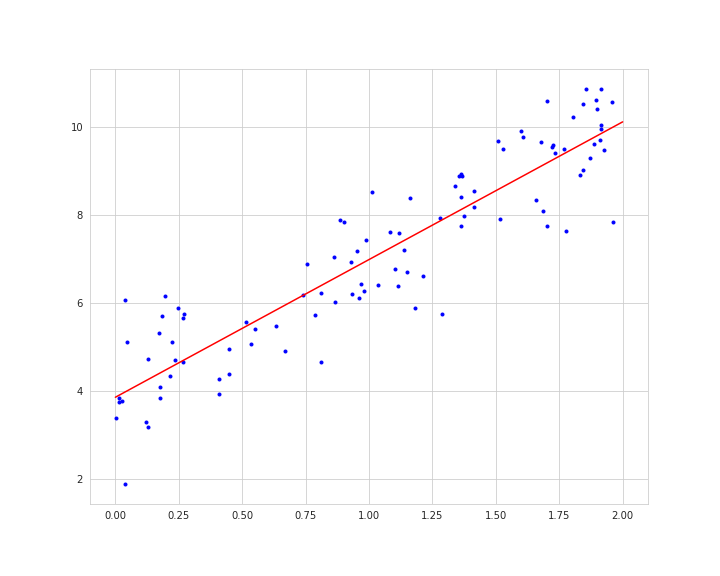
以下のように複雑なデータであっても直線を引こうとするので、上手く適合できないといった問題もあります。
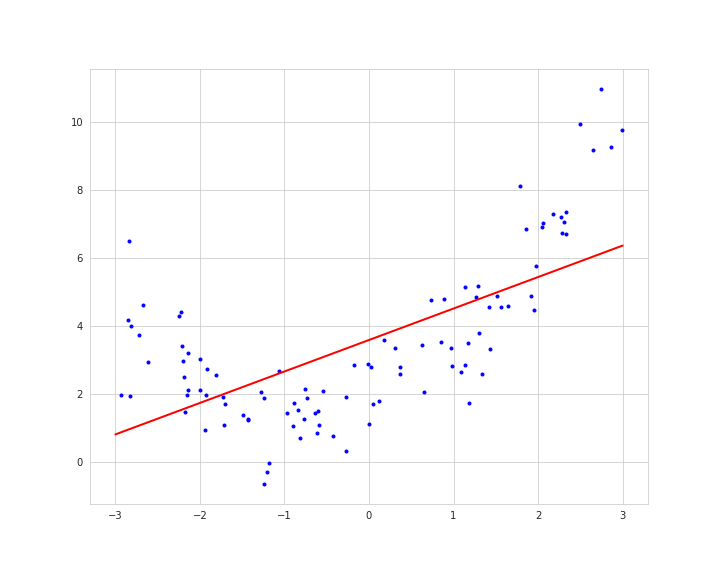
もし複雑なデータ(非線形)であった場合、それに合った複雑な機械学習モデルを適用することで、精度が向上する可能性もあります。
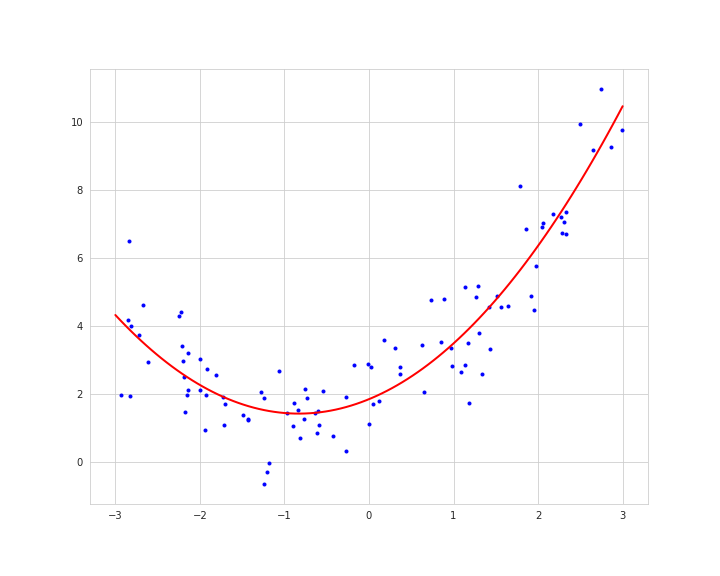
線形回帰モデルでの予測誤差を確認してみます。
# 実行
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lin_reg = LinearRegression().lin_reg.fit(X_s, y)
lin_pred = lin_reg.predict(X_s)
lin_mse = mean_squared_error(y, lin_pred)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
# 結果
0.5754619586800496
約±5万7千ドルの誤差です。
この数値よりも低い結果を出す機械学習モデルを使って訓練していきましょう。
今回使用するモデルは、SVM(サポートベクトルマシン)、RandomForest(ランダムフォレスト)、GradientBoostingTree(勾配ブースティング決定木)、MLP(マルチレイヤーパーセプトロン)の四つです。
これらは非常に人気の高い機械学習モデルとして使われているので、使い慣れておく必要があると思います。
個々のモデルは人気がありますが、難しい計算が行われたアルゴリズムなので、理論的な仕組みは別の記事にまとめていきます。
ここでは実装に集中できるよう進めて行きたいと思います。
他にもscikit-learnには様々なモデルが用意されているので、興味のある方は色々試してみてください。
SVM(サポートベクトルマシン)¶
SVMは、中小規模のデータセットに向いた、非常に多目的に活用できるモデルです。
分類問題、回帰問題、外れ値検出などにも使え、ハイパーパラメータの設定も色々と操作することのできる非常に柔軟なモデルです。
ではscikit-learnからSVRをインポートします。
from sklearn.svm import SVR
svm_reg = SVR()
svm_reg.fit(X_s, y)
では全体の予測値と正解ラベルの誤差を求めてみます。
# 実行
svm_pred = svm_reg.predict(X_s)
svm_mse = mean_squared_error(y, svm_pred)
svm_rmse = np.sqrt(svm_mse)
svm_rmse
# 結果
0.4970621662313961
誤差±4万9千ドルでした。
RandomForest(ランダムフォレスト)¶
ランダムフォレストは、もっとも強力なアルゴリズムのひとつとして有名な機械学習モデルのひとつです。
分類・回帰として実装することができ、その構成要素は、決定木という機械学習モデルをアンサンブル学習によって組み合わせたモデルです。
アンサンブル学習は複数のモデルを訓練し、回帰の場合は個々の予測結果の平均をして、最終的な予測値として出力します。
ではscikit-learnからRandomForestRegressorをインポートします。
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor(n_estimators=100, random_state=42)
forest_reg.fit(X_s, y)
全体の予測値と正解ラベルの誤差を求めてみます。
# 実行
forest_pred = forest_reg.predict(X_s)
forest_mse = mean_squared_error(y, forest_pred)
forest_rmse = np.sqrt(forest_mse)
forest_rmse
# 結果
0.1619785783725724
誤差±1万6千ドルでした。訓練セットに対してはかなり精度が良い感じです。
GradientBoostingTree(勾配ブースティング決定木)¶
勾配ブースティングは、複数の決定木を逐次的に訓練し、モデルの修正を試みながら予測を出していきます。
決定木1の予測値と正解ラベルの誤差を、決定木2の目的変数(正解ラベル)として渡し、訓練された決定木2の予測値と正解ラベルの誤差を、決定木3の目的変数として渡すというような段階を踏んで、最終的に決定木1、決定木2、決定木3の予測値の和を予測として返します。
こちらも分類・回帰の実装ができます。
ではscikit-learnからGradientBoostingRegressorをインポートします。
from sklearn.ensemble import GradientBoostingRegressor
gb_reg = GradientBoostingRegressor(random_state=42)
gb_reg.fit(X_s, y)
全体の予測値と正解ラベルの誤差を求めてみます。
# 実行
gb_pred = gb_reg.predict(X_s)
gb_mse = mean_squared_error(y, gb_pred)
gb_rmse = np.sqrt(gb_mse)
gb_rmse
#結果
0.4628402048901585
誤差±4万6千ドルでした。
MLP(マルチレイヤーパーセプトロン)¶
多層パーセプトロンは、複数の人工ニューロンの隠れ層からなる深層学習モデルです。
ニューロンとは、動物の大脳皮質で見られる細胞のことであり、それをコンピュータで表現されたのが人工ニューロンとなります。
ここでは簡単な説明に留めておきますが、これらの人工ニューロンはネットワーク状に接続されていることから人工ニューラルネットワーク(ANN)とも言われています。
複数の隠れ層では無い入力ニューロンと出力ニューロンだけのネットワーク構造を持つニューラルネットワークを単層パーセプトロン(パーセプトロン)と言い、その単純な構造から線形分離不可能な問題に対し限界に達していました。
そこで考えられたのが、パーセプトロンを積み上げするといったアプローチでした。
そして訓練方法はバックプロパゲーションというアルゴリズムを導入することにより、深層学習の基礎が築かれたということになります。
ニューラルネットワークでは、入力値が0から1までの範囲に収まっていることを前提にしていることが多いので、最小最大スケーリング(正規化)を施すことが有用と言われています。
最小最大スケーリングは値を0から1にスケーリングするだけです。scikit-learnのMinMaxScalerで実装することができます。
from sklearn.preprocessing import MinMaxScaler
min_max = MinMaxScaler()
X_m = min_max.fit_transform(X)
※scikit-learn公式ドキュメントを見る限り、StandardScalerの標準化で訓練を行っても問題無いようなので、ここでは全てのモデルに標準化された訓練データを扱います。
ではscikit-learnからMLPRegressorをインポートします。
from sklearn.neural_network import MLPRegressor
mlp_reg = MLPRegressor(max_iter=300, random_state=42)
mlp_reg.fit(X_s, y)
全体の予測値と正解ラベルの誤差を求めてみます。
# 実行
mlp_pred = mlp_reg.predict(X_s)
mlp_mse = mean_squared_error(y, mlp_pred)
mlp_rmse = np.sqrt(mlp_mse)
mlp_rmse
# 結果
0.4682285084580455
誤差±4万6千ドルでした。
それぞれのRMSEをpandasのデータフレームに格納し、見比べてみます。
# 実行
accuracy = pd.DataFrame([svm_rmse, forest_rmse, gb_rmse, mlp_rmse],
index=['SVM', 'RandomForest', 'GBoost', 'MLP'], columns=['Normal'])
accuracy

結果を見てみるとランダムフォレストが他と比べてずば抜けて誤差が低いことが分かります。
このような結果は過学習している可能性があります。もちろん今の時点ではテストセットで評価を行った訳ではないので過学習していない可能性もあります。
できればテストセットでの評価は1回切りにしたいので、検証セットを利用して各モデルの評価を行っていきたいと思います。
検証セットでの評価方法は2通りほどあり、1つはテストセットを分割した時のように、scikit-learnのtrain_test_splitを使用する。
もう1つは、何個かの数に訓練セットを分割し、分割されたデータで訓練・評価を分割された個数分行い、その平均値を取るという方法です。この方法は交差検証と言ってscikitt-learnのcross_val_scoreで実装することができます。
今回は後者の交差検証を行って、各モデルの誤差を再確認してみます。
交差検証を使って再度評価を行う¶
それでは改めて交差検証の内容を説明していきたいと思います。
交差検証は訓練データを幾つかの数に分割し、その分割された分だけ訓練・評価(平均二乗誤差)を行いその平均値をモデルの精度として表します。
例えば、5分割するのであれば、1つ目のサブセットを評価用として取り除き、残り4つのサブセットを訓練用として1回の学習を終えます。次は前と異なるサブセット、つまり2つ目のサブセットを評価用とし、余った残りの4つのサブセットを訓練用として2回目の学習を終えます。
この工程を5回繰り返し5つの精度が決まるので、その精度の平均値が実際の性能指標ではないか?ということになります。
ではさっそくSVMから再度評価を行ってみます。
SVM(交差検証)¶
交差検証はscikit-learnのcross_val_scoreで簡単に実装できます。
# 実行
from sklearn.model_selection import cross_val_score
# scornigは評価方法。ここでは平均二乗誤差
# cvは検証回数
svm_scores = cross_val_score(svm_reg, X_s, y, scoring='neg_mean_squared_error', cv=5)
svm_scores
# 結果
array([-0.26514347, -0.25648105, -0.25977195, -0.27082487, -0.27898093])
scikit-learnの交差検証では負数(マイナス)の平均二乗誤差が求められるので、平方根をとる際にマイナスを掛けてあげます。
svm_rmse_score = np.sqrt(-svm_scores)
評価・平均・標準偏差を出力する関数を定義しておきます。
def display_scores(scores):
print('Score: ', scores)
print('\n')
print('Mean: ', scores.mean())
print('\n')
print('Standard deviation: ', scores.std())
検証結果が与えられた変数を関数に渡します。
# 実行
display_scores(svm_rmse_score)
# 結果
Score: [0.51492083 0.50643958 0.50967828 0.52040836 0.52818645]
Mean: 0.5159267044471152
Standard deviation: 0.007751731446256992
前のモデルより少し精度が落ちています。
検証の回数を増やすことによって、さらに厳しく評価を行えるかと思います。
RandamForest(交差検証)¶
# 実行
forest_scores = cross_val_score(forest_reg, X_s, y, scoring='neg_mean_squared_error', cv=5)
forest_rmse_score = np.sqrt(-forest_scores)
display_scores(forest_rmse_score)
# 結果
Score: [0.43767776 0.44131438 0.42937464 0.44081916 0.44592454]
Mean: 0.43902209575948004
Standard deviation: 0.005495606730974703
ランダムフォレストは前の時よりもかなり精度が落ちています。
GradientBoosting(交差検証)¶
# 実行
gb_scores = cross_val_score(gb_reg, X_s, y, scoring='neg_mean_squared_error', cv=5)
gb_rmse_score = np.sqrt(-gb_scores)
display_scores(gb_rmse_score)
# 結果
Score: [0.47825225 0.4643197 0.46411158 0.4858653 0.48045377]
Mean: 0.4746005207534713
Standard deviation: 0.008834071900714249
MLP(交差検証)¶
# 実行
mlp_scores = cross_val_score(mlp_reg, X_s, y, scoring='neg_mean_squared_error', cv=5)
mlp_rmse_score = np.sqrt(-mlp_scores)
display_scores(mlp_rmse_score)
# 結果
Score: [0.49511224 0.48278609 0.48395667 0.5037626 0.50544144]
Mean: 0.4942118094125941
Standard deviation: 0.009527304188063277
では各モデルの検証結果をデータフレームに格納します。
# 実行
accuracy['CrossValidation'] = [svm_rmse_score.mean(),
forest_rmse_score.mean(),
gb_rmse_score.mean(),
mlp_rmse_score.mean()]
accuracy
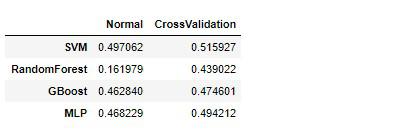
ランダムフォレスト以外のモデルは、そこまで大きく差は開いていませんでした。
このデータに対しては優秀なモデルと言えるかもしれません。
しかし、まだ各モデルのハイパーパラメータを色々試していないので、どの程度性能が向上するか試してみる必要はあります。
各モデルには多数のハイパーパラメータ値を設定することができますが、それぞれ特定の設定を1回ずつ試すには時間がかかりますし面倒です。
それらの問題を解消するために、scikit-learnのGridSearchCVとRandomizedSearchCVを使って、最良のハイパーパラメータ値の組み合わせを実装していきます。
グリッドサーチとランダムサーチ¶
グリッドサーチとランダムサーチは与えられたハイパーパラメータ値をそれぞれの組み合わせで交差検証し、最高の組み合わせを導き出してくれる非常に高機能なツールです。
両者の違いは、ハイパーパラメータ値の探索領域が少ないか多いかです。
少ない組み合わせで試してみたい場合はグリッドサーチを使い、組み合わせが多い場合はランダムサーチを使うと良いかと思います。
ではグリッドサーチの方から実装していきたいと思います。
SVM(グリッドサーチ)¶
ハイパーパラメータに関しては、こちらをご参考ください。
下記の実装では、param_gridというリスト内の辞書にハイパーパラメータ値を幾つか設定します。そしてSVMを初期化し、GridSearchCVの引数に、モデル、ハイパーパラメータ群、検証回数、評価設定を渡し、訓練を開始します。
from sklearn.model_selection import GridSearchCV
# C: 正則化の強度
# kernel: カーネル関数
param_grid = [
{'C': [0.001, 0.01, 1, 10],
'gamma': ['auto', 'scale'],
'kernel': ['rbf', 'linear']}
]
svm_reg = SVR()
# cvは交差検証、scoringは評価方法
svm_grid_search = GridSearchCV(svm_reg, param_grid, cv=5, scoring='neg_mean_squared_error')
svm_grid_search.fit(X_s, y)
どのように訓練されたかというと、ハイパーパラメータ値はそれぞれCでは3つ、gammaでは2つ、kernelでは2つの設定を行っているので、全ての組み合わせを試すと12通りの訓練が行われています。
そして1通りずつ交差検証を5回(5分割)行っているので、計60回訓練・評価が行われています。
結果12通りの検証平均値が出力されます。
訓練が終了したら、最高の組み合わせを確認してみます。
# 実行
svm_grid_search.best_params_
# 結果
{'C': 10, 'gamma': 'auto', 'kernel': 'rbf'}
他にも各ハイパーパラメータ値を確認できる属性が用意されているので、詳しく知りたい方は公式ドキュメントをご参考ください。
ではSVMの最高推定器を使って誤差を確認してみます。
# 実行
svm_grid_pred = svm_grid_search.best_estimator_.predict(X_s)
svm_grid_mse = mean_squared_error(y, svm_grid_pred)
svm_grid_rmse = np.sqrt(svm_grid_mse)
svm_grid_rmse
# 結果
0.4667832146849868
これまでのSVMモデルの中で最高のモデルが手に入りました。
RandomForest(グリッドサーチ)¶
SVMと同じ要領でハイパーパラメータ値を幾つか設定します。
RandomForest回帰のハイパーパラメータ:公式ドキュメント
# max_depth: 最大ノード数
# n_estimators: 決定木の個数
param_grid = [
{'max_depth': [5, 6, 7],
'n_estimators': [300, 400, 500],
'random_state': [42]}
]
# このように辞書を分割して作成することもできる
"""
param_grid = [
{'bootstrap': [True], ......, .......},
{'bootstrap': [False], ....., ......},
]
"""
forest_reg = RandomForestRegressor()
forest_grid_search = GridSearchCV(forest_reg, param_grid, cv=5, scoring='neg_mean_squared_error')
forest_grid_search.fit(X_s, y)
最高のハイパーパラメータ値を確認
# 実行
forest_grid_search.best_params_
# 結果
{'max_depth': 7, 'n_estimators': 400, 'random_state': 42}
平均二乗平方根誤差(RMSE)で評価
# 実行
forest_grid_pred = forest_grid_search.best_estimator_.predict(X_s)
forest_grid_mse = mean_squared_error(y, forest_grid_pred)
forest_grid_rmse = np.sqrt(forest_grid_mse)
forest_grid_rmse
# 結果
0.47944300298066644
GradientBoosting(グリッドサーチ)¶
GradientBoosting回帰のハイパーパラメータ:公式ドキュメント
# max_depth: 最大ノード数
# n_estimators: 決定木の個数
param_grid = [
{'max_depth': [5, 6, 7],
'n_estimators': [300, 400, 500],
'random_state': [42]}
]
gb_reg = GradientBoostingRegressor()
gb_grid_search = GridSearchCV(gb_reg, param_grid, cv=5, scoring='neg_mean_squared_error')
gb_grid_search.fit(X_s, y)
最高のハイパーパラメータ値を確認
# 実行
gb_grid_search.best_params_
# 結果
{'max_depth': 7, 'n_estimators': 500, 'random_state': 42}
平均二乗平方根誤差(RMSE)で評価
# 実行
gb_grid_pred = gb_grid_search.best_estimator_.predict(X_s)
gb_grid_mse = mean_squared_error(y, gb_grid_pred)
gb_grid_rmse = np.sqrt(gb_grid_mse)
gb_grid_rmse
# 結果
0.13605815102288582
この組み合わせはかなり性能が良いようにですね。
MLP(ランダムサーチ)¶
ニューラルネットワークのMLP(マルチレイヤーパーセプトロン)ではランダムサーチを使ってハイパーパラメータ値を幾つか設定してみたいと思います。
グリッドサーチと同じ要領で使えますが、ランダムサーチではランダムなハイパーパラメータ値の組み合わせで評価が行われます。
デフォルトでは10個までの組み合わせとなっていますが、探索領域が大きい場合などは回数を指定して評価を行うことができます。
結果は交差検証を行っているので、組み合わせ分の平均値がそれぞれ出力されます。
ではさっそく実装していきます。
# hidden_layer_sizes: ニューロンと層の数
# max_iter: 訓練の回数
param_random = {'hidden_layer_sizes': [(100),
(100, 100),
(50, 50, 50),
(20, 50, 80, 50, 20),
(20, 30, 50, 30, 20, 10)],
'max_iter': [300, 1000],
'random_state': [42]}
mlp_reg = MLPRegressor()
# n_jobs: -1は全てのプロセッサを使用する
# n_iter: デフォルトでは10の組み合わせとなっている
mlp_random_search = RandomizedSearchCV(mlp_reg,
param_random,
cv=5,
n_jobs=-1,
scoring='neg_mean_squared_error',
random_state=42)
mlp_random_search.fit(X_s, y)
最高のハイパーパラメータ値を確認
# 実行
mlp_random_search.best_params_
# 結果
{'random_state': 42, 'max_iter': 300, 'hidden_layer_sizes': 100}
平均二乗平方根誤差(RMSE)で評価
# 実行
mlp_random_pred = mlp_random_search.best_estimator_.predict(X_s)
mlp_random_mse = mean_squared_error(y, mlp_random_pred)
mlp_random_rmse = np.sqrt(mlp_random_mse)
mlp_random_rmse
# 結果
0.4682285084580455
それぞれの結果が解かったと思うので、データフレームに格納して比べてみましょう。
# 実行
accuracy['Grid_or_Random_Search'] = [svm_grid_rmse,
forest_grid_rmse,
gb_grid_rmse,
mlp_random_rmse]
accuracy
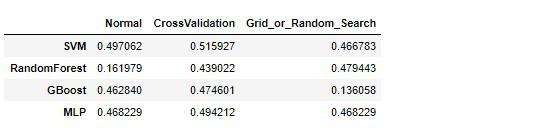
各モデルでの最高のハイパーパラメータ値の組み合わせでは、勾配ブースティング決定木(GradientBoostingTree)がずば抜けて高い精度を出しています。
最高のモデル達が出そろった所で、さらに交差検証をかけて精度を確認してみたいと思います。
最高推定器での交差検証&最良の機械学習モデルで最後の評価¶
最後に、出揃った最高の各機械学習モデルを交差検証にかけて、一番最良だった機械学習モデルでテストセットでの評価を行っていきたいと思います。
グリッドサーチやランダムサーチを行った推定器のbest_estimator_属性を使用して、それぞれ交差検証を行っていきます。
SVM(最高推定器での交差検証)¶
# 実行
svm_scores = cross_val_score(svm_grid_search.best_estimator_, X_s, y, scoring='neg_mean_squared_error', cv=5)
svm_best_rmse_score = np.sqrt(-svm_scores)
display_scores(svm_best_rmse_score)
# 結果
Score: [0.50802572 0.49847396 0.50282046 0.50834014 0.5181417 ]
Mean: 0.5071603973281642
Standard deviation: 0.006588154003046403
RandomForest(最高推定器での交差検証)¶
# 実行
forest_scores = cross_val_score(forest_grid_search.best_estimator_, X_s, y, scoring='neg_mean_squared_error', cv=5)
forest_best_rmse_score = np.sqrt(-forest_scores)
display_scores(forest_best_rmse_score)
# 結果
Score: [0.51780804 0.50198563 0.50527514 0.51992336 0.51482569]
Mean: 0.5119635710774529
Standard deviation: 0.0070710987015029335
GradientBoosting(最高推定器での交差検証)¶
# 実行
gb_scores = cross_val_score(gb_grid_search.best_estimator_, X_s, y, scoring='neg_mean_squared_error', cv=5)
gb_best_rmse_score = np.sqrt(-gb_scores)
display_scores(gb_best_rmse_score)
# 実行
Score: [0.40716737 0.41110577 0.40223102 0.40498578 0.41716877]
Mean: 0.4085317400346223
Standard deviation: 0.005203044350615787
MLP(最高推定器での交差検証)¶
# 実行
mlp_scores = cross_val_score(mlp_random_search.best_estimator_, X_s, y, scoring='neg_mean_squared_error', cv=5)
mlp_best_rmse_score = np.sqrt(-mlp_scores)
display_scores(mlp_best_rmse_score)
# 結果
Score: [0.49511224 0.48278609 0.48395667 0.5037626 0.50544144]
Mean: 0.4942118094125941
Standard deviation: 0.009527304188063277
それぞれの結果をデータフレームに格納します。
# 実行
accuracy['Search_CV'] = [svm_best_rmse_score.mean(),
forest_best_rmse_score.mean(),
gb_best_rmse_score.mean(),
mlp_best_rmse_score.mean()]
accuracy
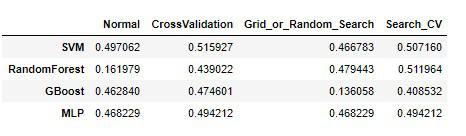
最終的に、勾配ブースティング決定木(GradientBoostingTree)の精度が最も良いものとなりました。
これまでの各モデルの結果を平均してみます。
# 実行
accuracy.mean(axis=1).sort_values()
# 結果
GBoost 0.370508
RandomForest 0.398102
MLP 0.481220
SVM 0.496733
dtype: float64
この結果を見る限りでは、上位2つは過学習組と下位2つは過小適合組のように別れました。
過学習の心配はありますが、一番良い精度のモデルである勾配ブースティング決定木でテストセットの評価を行います。
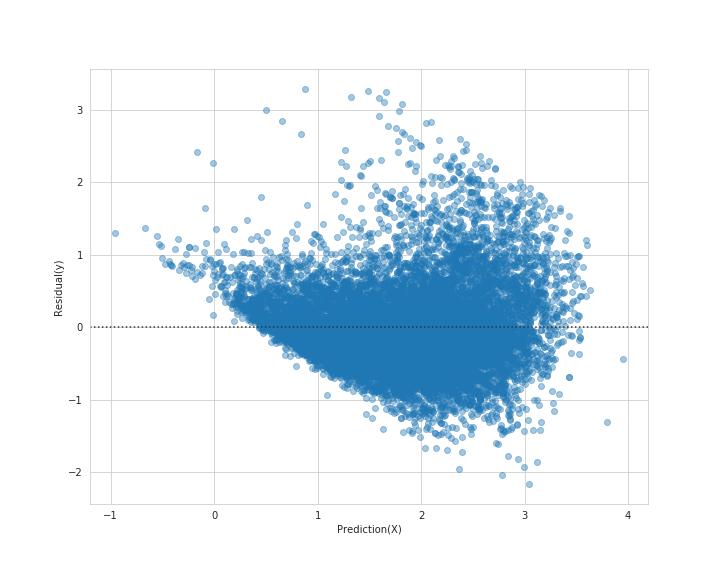
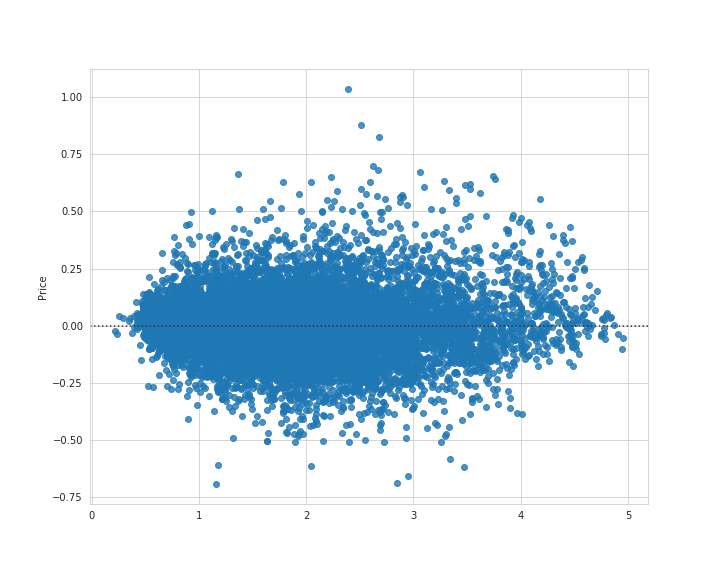
その前に残差プロットを見てみます。
# 実行
plt.figure(figsize=(10, 8))
sns.residplot(gb_grid_pred, y - gb_grid_pred)
plt.savefig('gb_train_resid.png')
plt.show()
ではこの中で最も最良であるモデルを使ってテストセットを評価していきたいと思います。
※誤ってscaler.fit_transform(X_test)とテストセットに対して平均と標準の計算をし直してしまったため(正確にはscaler.transform(X_test))、依然と結果は大きく変わりました。なのでここから大幅に内容を変更させて頂きました。
# 実行
X_test, y_test = custom_conversion(test_set)
X_test_s = scaler.transform(X_test)
best_pred = gb_grid_search.best_estimator_.predict(X_test_s)
best_mse = mean_squared_error(y_test, best_pred)
best_rmse = np.sqrt(best_mse)
best_rmse
# 結果
0.3940852085095778
結果のRMSEは0.39、つまり訓練セットでの交差検証ではおよそ0.40でしたので、素晴らしい評価となりました。
残差プロットを見てみます。
# 実行
plt.figure(figsize=(10, 8))
sns.residplot(best_pred, y_test - best_pred)
plt.savefig('gb_test_resid.png')
plt.show()
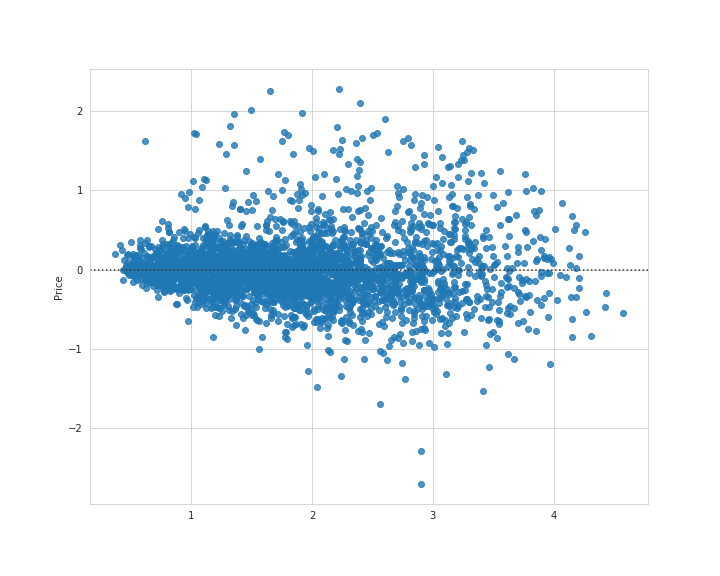
残差を見ても、中央にまとまっているのが分かります。
下方に外れ値のような分布も見受けられますが、多くの分布が0付近集まっているので良い結果と言えるかと思います。
このモデルをpickleファイルに保存して、いつでも使えるようにしておきます。
最良のモデルをpickleファイルに保存¶
pickleファイルへの保存では、幾つか方法がありますが、ここではwith文を使用して保存していきます。
import pickle
with open('best_model.pickle', 'wb') as f:
pickle.dump(gb_grid_search.best_estimator_, f)
openにより書き込み用のファイルを準備(開く)して、書き込みモード(wb)を指定します。
そのファイルをfという変数に入れ、pickle.dump()の第1引数に書き込みたい要素、第2引数にファイルを置きます。
ファイルは実行された階層(ディレクトリ)に置かれているので、そのファイルを再び読み込んでみます。
読み込み
open時、ファイルをバイナリ形式(rb)に書き込んでからfに代入。
# 実行
with open('best_model.pickle', 'rb') as f:
best_model = pickle.load(f)
best_model
# 結果
GradientBoostingRegressor(alpha=0.9, criterion='friedman_mse', init=None,
learning_rate=0.1, loss='ls', max_depth=7,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=500,
n_iter_no_change=None, presort='auto',
random_state=42, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
今回は最良のモデルを選び出すために交差検証を行って過学習モデルを検出していきました。
過学習モデルは複雑なアルゴリズムが故に自由度が高いため、訓練データに対して過剰に適合しようとしてしまいます。
逆に線形回帰モデルのような単純なアルゴリズムでは前提が敷かれているため(バイアス)、データによっては過小適合しやすい傾向にあります。
これらはバイアスと分散のトレードオフという関係性があります。
バイアスと分散のトレードオフ¶
モデルの前提に無視したデータ、つまりモデルは線形なのに与えるデータは2次元データなど、前提条件のある偏り(バイアス)の高いモデルは、訓練データに対し過小適合しやすい。
訓練セットとテストセットの両方で過小適合しやすいが、汎化性能は高い。つまり過学習を起こしにくい傾向にあるといいます。
もう一方で、モデルの前提条件を踏まえず、データの小さな差異にまで敏感に学習するモデル、つまり自由度の高すぎるモデル(SVM、RandomForest、GradientBoost、MultiLayerPerceptronなど)では分散が高くなりがちで過学習を引き起こしやすいという傾向にあります。
ということで、この前者と後者ではトレードオフの関係にあると言われている。
課題¶
今回はランダムサーチでいくつものハイパーパラメータを試し、さらに交差検証を使って厳しく評価をおこなってきましたが、第4回では別のアプローチで過学習モデルの検証をしていきたいと思います。
次への課題
- 検証セット作る
- 学習曲線をみて汎化性能を他モデルと比べる
- 正則化を強めて検証してみる
【第4回カリフォルニア住宅価格の予測】学習曲線を利用して各モデルの汎化性能を検証
それでは以上となります。
最後までご覧いただきありがとうございました。
