【第4回カリフォルニア住宅価格の予測】学習曲線を利用して各モデルの汎化性能を検証
投稿日 2020年4月25日 >> 更新日 2024年7月9日
※誤ってscaler.fit_transform(X_test)とテストセットに対して平均と標準の計算をし直してしまったため(正確にはscaler.transform(X_test))、依然と結果は大きく変わりましたので、後半の内容を変更させて頂きました。
今回はカリフォルニア住宅価格の予測第4回ということで、学習曲線を利用した各機械学習モデルの汎化性能を検証していきたいと思います。
前回の第3回目では、最良の機械学習モデルを選び出すために、4つのモデル(SVM・RandomForest・GradientBoostingTree・MLP(マルチレイヤーパーセプトロン))で訓練を行い、各モデルがしっかり汎化されているのかを検証するために交差検証を行って過学習の度合いを見ていきました。
【第3回カリフォルニア住宅価格の予測】最良の機械学習モデルを選び評価を行う
最終的に以下4種類の訓練誤差(RMSE)が揃い
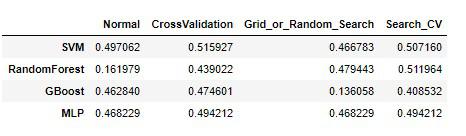
※線形回帰モデルではRMSE約0.57。
- Normal(デフォルト値のハイパーパラメータでの訓練誤差)
- CrossValidation(交差検証を5分割で行った平均値の検証誤差)
- Grid_or_Random_Search(グリッドサーチやランダムサーチでハイパーパラメータを設定した最高推定器の検証誤差)
- Search_CV(最高推定器での交差検証を行った検証誤差)
どのモデルがもっとも最良か、という指標をこのデータフレームの数値を頼りに決めていきました。
結果は最高推定器版のGradientBoostingTreeに交差検証を行ったRMSEが0.40と性能が高かったので、このモデルを使用してテストセットでの評価を行いました。
テストセットのRMSEは0.39ということもあり、汎化性能は高かったと見受けられることができました。
前回は交差検証での過学習モデルの検知、今回はグラフに学習曲線を描いて訓練誤差と検証誤差の様子を見てモデル選びの判断を行いたいと思います。
分散の高い過学習の傾向があるモデルには、正則化ハイパーパラメータの強度を強めて検証もしていきたいと思います。
実行環境&使用ライブラリ¶
| 実行環境 |
|---|
| Windows Subsystem for Linux |
| Python 3.6.9 |
| pip 9.0.1 |
| Jupyter notebook |
| 使用ライブラリ | ライセンス |
|---|---|
| numpy==1.16.4 | OSI Approved (new BSD) |
| pandas==0.25.0 | BSD |
| matplotlib==3.1.1 | PSF |
| seaborn==0.9.0 | BSD |
| scikit-learn==0.21.3 | OSI Approved (new BSD) |
データの準備¶
機械学習モデルに適用させるまでは、第3回カリフォルニア住宅価格の予測と一緒なので、「データの準備」をご覧になってからこちらに戻ってきてください。
検証セットを使って学習曲線を描く¶
データの準備ができたところで、さっそく学習曲線について見ていきたいと思います。
学習曲線というのは、訓練セットと検証セットを用意して、それぞれの学習の進み具合をグラフで見て検証を行うことです。
ただ学習を行うのではなく、訓練セットだけを順番に1つのデータから機械学習モデルへ流し、検証セット(未知のデータ)の誤差を出すというアプローチです。
訓練セットのデータ数をだんだん増やしていき、それに伴って検証セットで誤差を出し続ける。検証セットは最初から最後まで全て枚数を使うので、最初は全く汎化されない。
しかし上手く行けば、訓練セットが増えるにつれて訓練誤差と検証誤差(汎化誤差)は縮んでいくはずなのであります。
実際に線形回帰モデルを使ってグラフを見てみます。
※説明変数のX_sは標準化済み(データの準備にて)
# 実行
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lin_reg = LinearRegression()
lin_pred = lin_reg.predict(X_s)
lin_mse = mean_squared_error(y, lin_pred)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
# 結果
0.5754619586800496
訓練セット全体のRMSEは0.57です。
ではscikit-learnのtrain_test_splitを使って訓練セットと検証セットに分割します。
from sklearn.model_selection import train_test_split
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=10)
機械学習モデルの訓練は、イテレーションをしながら10個目のデータからn個(最後)までの訓練セットのデータを100刻みで流していきます。
10個を100刻みにした理由は、後々の訓練で時間が掛かるからです。
10個は10束という事ではなく、1から10までの訓練データが終わったら、1から110までの訓練データで行うという意味です。
それらの結果を受け取るために、訓練用と検証用の空リストを作成しておきます。
# 訓練用と検証用の結果を納める
train_errors, val_errors = [], []
# 10個目のデータから順に、10、110と100個飛ばして回す
for m in range(10, len(X_train), 100):
# 順番に110, 210, 310, ...、と訓練し、検証セットとの汎化誤差を比べる
lin_reg.fit(X_train[:m], y_train[:m])
y_train_predict = lin_reg.predict(X_train[:m])
y_val_predict = lin_reg.predict(X_val)
train_mse = mean_squared_error(y_train[:m], y_train_predict)
val_mse = mean_squared_error(y_val, y_val_predict)
train_rmse = np.sqrt(train_mse)
val_rmse = np.sqrt(val_mse)
# それぞれのRMSEをリストに収める
train_errors.append(train_rmse)
val_errors.append(val_rmse)
それぞれの結果がリストに収められたと思うので、グラフに描画してみます。
# 実行
import matplotlib.pyplot as plt
# 画像サイズ
plt.figure(figsize=(15, 8))
# 訓練セット
plt.plot(train_errors, "r-+", alpha=0.5, linewidth=2, label="Train")
# 検証セット
plt.plot(val_errors, "b-", alpha=0.5, linewidth=3, label="Validation")
# 凡例
plt.legend(loc="upper right", fontsize=14)
# x軸の名前
plt.xlabel("Train set size", fontsize=14)
# y軸の名前
plt.ylabel("RMSE", fontsize=14)
# x軸のメモリは0からtrain_errorsサイズを指定
# y軸のメモリは0から0.7に指定(この範囲にだいたい分布がされるので)
plt.axis([0, len(train_errors), 0, 0.7])
plt.savefig('Linear_error.png')
plt.show()
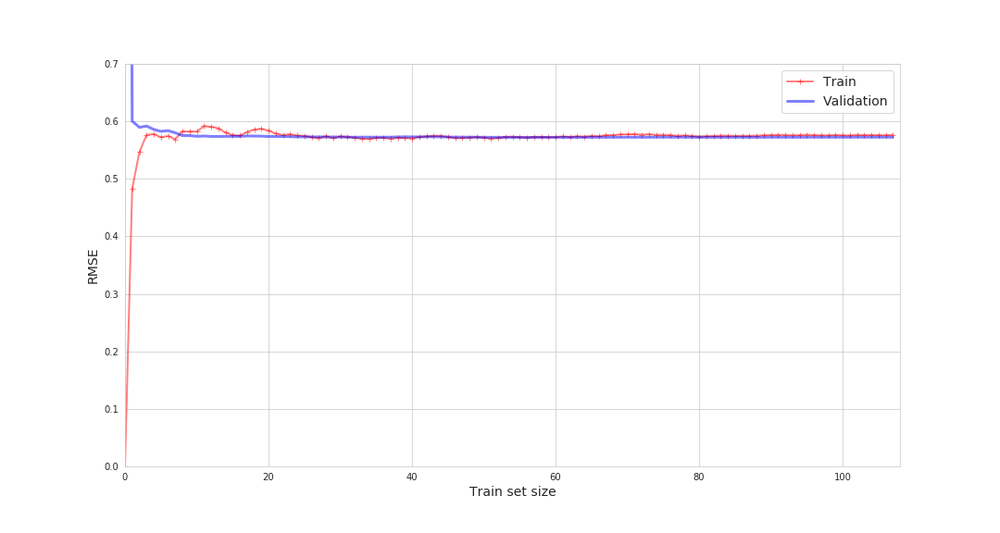
赤色が訓練セット、青色が検証セット。
線形回帰モデルは他の複雑なモデルと比べて過小適合していますが、汎化性能は高く、理想的なグラフだと個人的には思います。
最初に訓練セットと検証セットの誤差結果が離れているのは、訓練セット10個に対して検証セットの誤差を出しているので当たり前と言えます。
しかしだんだんその距離は縮まっていき差が殆どなくなりつつあります。
このような描画を、他の4つモデル(SVM・RandomForest・GradientBoostingTree・MLP)で試して行きたいと思います。
そのまえに、学習曲線用の関数を定義します。
訓練誤差と検証誤差の誤差を知りたいので、それ用に空リストを準備し、4つのモデルを流せるように少し変更します。
※訓練誤差と検証誤差の結果が欲しい方は、別途空リストを用意しましょう。
# データフレーム用の空リスト
# 訓練誤差と検証誤差の誤差を格納
generalization_error = []
# model_nameにモデル名を入れる
def plot_learning_curves(model, X, y, model_name=None):
# japanize_matplotlibで日本語設定
import japanize_matplotlib
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=10)
train_errors, val_errors = [], []
# 10個目のデータから順に、110、210と310個飛ばして回す
for m in range(10, len(X_train), 100):
# 順番に10, 110, 210, ...、と訓練し、検証誤差を出す
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_mse = mean_squared_error(y_train[:m], y_train_predict)
val_mse = mean_squared_error(y_val, y_val_predict)
train_rmse = np.sqrt(train_mse)
val_rmse = np.sqrt(val_mse)
# それぞれのRMSEをリストに収める
train_errors.append(train_rmse)
val_errors.append(val_rmse)
# それぞれの一番最終のRMSEの誤差を出す
train_val_error = np.round(train_errors[-1] - val_errors[-1], 4)
# 訓練誤差と検証誤差の誤差を絶対値に置き換える
train_val_error = np.abs(train_val_error)
# データフレーム用の空リストに収める
generalization_error.append(train_val_error)
plt.figure(figsize=(15, 8))
plt.plot(train_errors, "r-+", alpha=0.5, linewidth=2, label="訓練セット")
plt.plot(val_errors, "b-", alpha=0.5, linewidth=3, label="検証セット")
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("訓練セットの数", fontsize=14)
plt.ylabel("RMSE", fontsize=14)
# 最終のRMSEと、訓練・検証の差をタイトルに表示。
plt.title('{0}の訓練セット誤差:{1}、検証セット誤差:{2}、その差は{3}'.format(model_name,
np.round(train_errors[-1], 4),
np.round(val_errors[-1], 4),
train_val_error), fontsize=18)
plt.axis([0, len(train_errors), 0, 0.7])
plt.savefig('{}_error.png'.format(model_name))
plt.show()
SVMの学習曲線¶
所要時間約6分掛かります(CPU)。
# 実行
from sklearn.svm import SVR
svm_reg = SVR(gamma='auto')
plot_learning_curves(svm_reg, X_s, y, model_name='SVM')
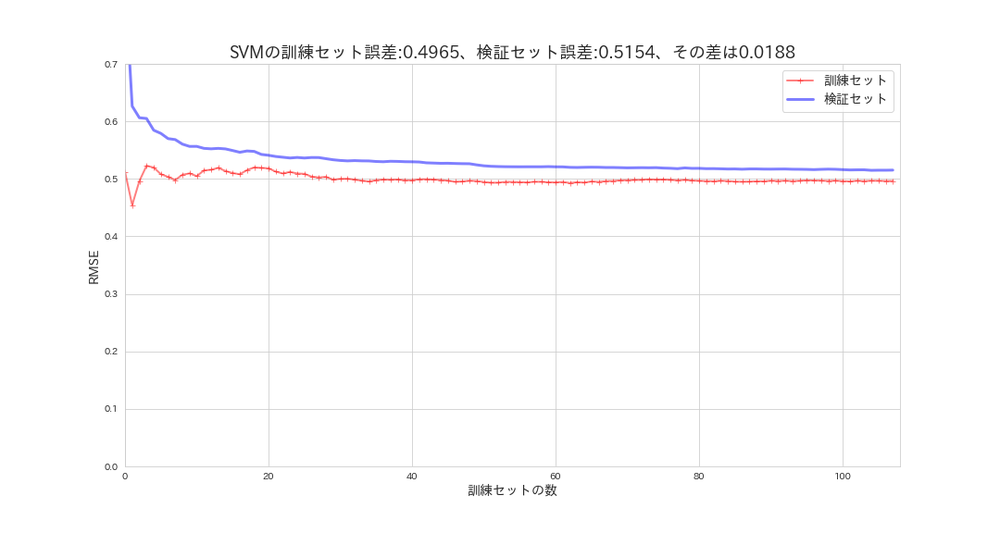
訓練誤差と検証誤差の誤差は、約0.02と中々良く汎化されています。
RandomForestの学習曲線¶
所要時間約4分(CPU)
# 実行
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor(n_estimators=100, random_state=42)
plot_learning_curves(forest_reg, X_s, y, model_name='RandomForest')
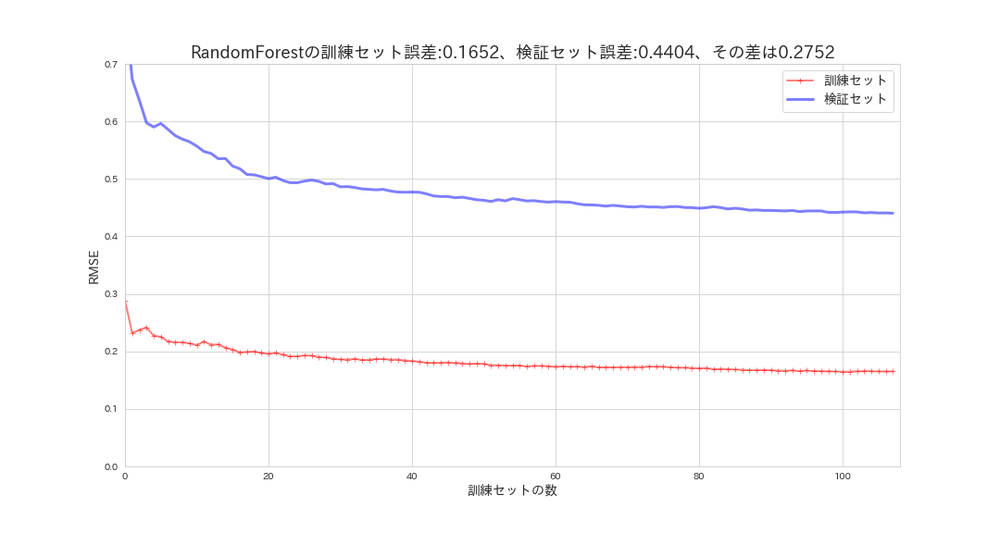
訓練セットの性能はもの凄く良いですが、検証セットの汎化性能はもの凄く低いことになっています。
いわゆる過学習モデルと言われるものです。
GradientBoostingsTreeの学習曲線¶
所要時間約1分(CPU)
# 実行
from sklearn.ensemble import GradientBoostingRegressor
gb_reg = GradientBoostingRegressor(random_state=42)
plot_learning_curves(gb_reg, X_s, y, model_name='GBoost')
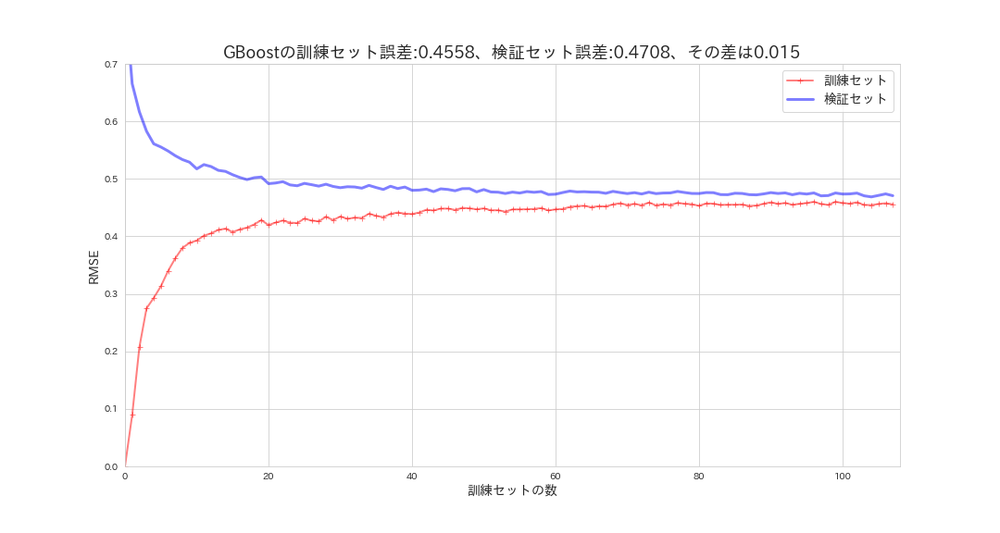
このモデルは理想的な曲線を描いています。
SVMよりも性能は良さそうです。
MLPの学習曲線¶
所要時間約10分(CPU)
# 実行
from sklearn.neural_network import MLPRegressor
mlp_reg = MLPRegressor(max_iter=1500, random_state=42)
plot_learning_curves(mlp_reg, X_s, y, model_name='MLP')
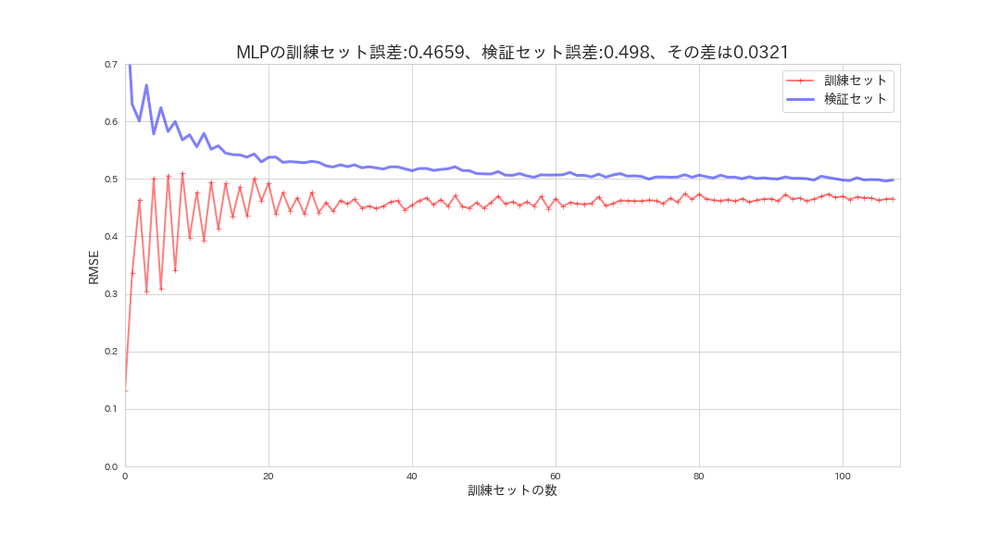
全体の評価は良いかもしれませんが、検証誤差(汎化誤差)との差はSVMの方が少ないので、五分五分だと思います。
では改めて、訓練誤差と検証誤差の誤差がgeneralization_errorリストに格納されていると思いますので、pandasのデータフレームにして確認してみます。
# 実行
import pandas as pd
df_error = pd.DataFrame(generalization_error,
index=['SVM', 'RandomForest', 'GBoost', 'MLP'],
columns=['Normal'])
df_error

各モデルの訓練誤差と検証誤差の誤差はRandomForestを除いて低い(中々良い)結果となりました。
もしかすると正則化ハイパーパラメータを制御することによって、誤差が縮まるかもしれません。正則化ハイパーパラメータは自由度を制御する、つまり分散を下げるので過学習を起こしにくくなります。
第3回でも行ったランダムサーチを使用して、複数のハイパーパラメータを設定し訓練を再度実行してみます。
SVM(ランダムサーチ)の学習曲線¶
所要時間約13分(CPU)
from sklearn.model_selection import RandomizedSearchCV
# kernel: ガウスRBFカーネル・線形カーネル・多項式カーネル
# C: 正則化ハイパーパラメータ、小さくすると制御を強める
# degree: 多項式回帰の次元設定
param_random = {
'kernel': ['rbf', 'linear', 'poly'],
'C': [0.001, 0.01, 1],
'degree': [2],
'gamma': ['auto'],
}
svm_reg = SVR()
svm_random_search = RandomizedSearchCV(svm_reg,
param_random,
cv=5,
scoring='neg_mean_squared_error',
n_iter=9,
random_state=42)
svm_random_search.fit(X_s, y)
svm_random_search.best_params_
# 結果
{'kernel': 'rbf', 'gamma': 'auto', 'degree': 2, 'C': 1}
所要時間約6分(CPU)
※generalization_errorの中身を空にしておきます。
# 実行
generalization_error = []
plot_learning_curves(svm_random_search.best_estimator_, X_s, y, model_name='best_SVM')
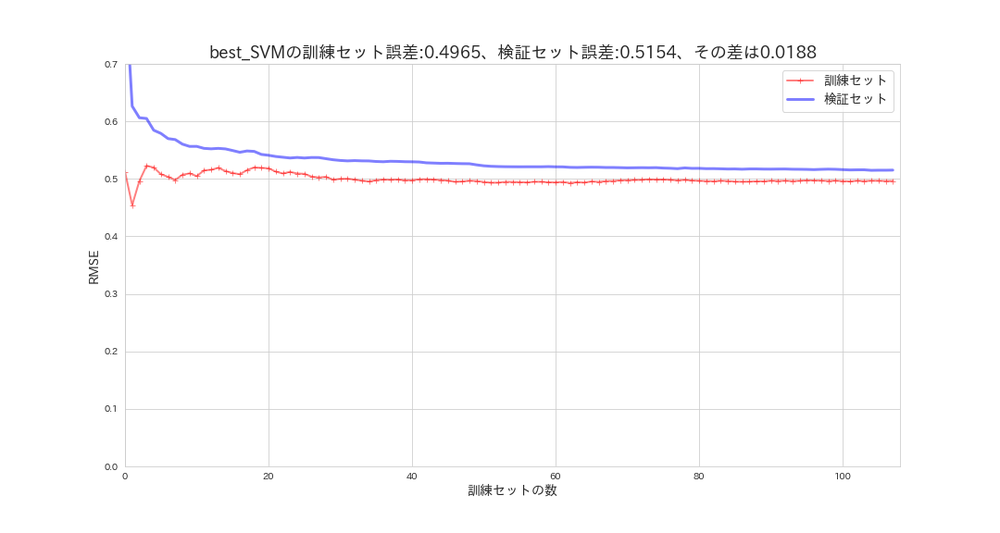
最高の推定器をサーチした結果、デフォルトのハイパーパラメータと変わらないので、学習曲線も同じとなりました。
RandomForest(ランダムサーチ)の学習曲線¶
所要時間約2分(CPU)
# max_depth: 最大ノード数(正則化の制御、多項式回帰のdegreeのようなもの)
# n_estimators: 決定木の個数
random_search = {'max_depth': [1, 2],
'n_estimators': [300, 500, 1000, 2000],
'random_state': [42]}
forest_reg = RandomForestRegressor()
forest_random_search = RandomizedSearchCV(forest_reg,
random_search,
cv=5,
n_jobs=-1,
scoring='neg_mean_squared_error',
n_iter=8,
random_state=42)
forest_random_search.fit(X_s, y)
forest_random_search.best_params_
# 結果
{'random_state': 42, 'n_estimators': 500, 'max_depth': 2}
所要時間約3分(CPU)
# 実行
plot_learning_curves(forest_random_search.best_estimator_, X_s, y, model_name='best_RandomForest')
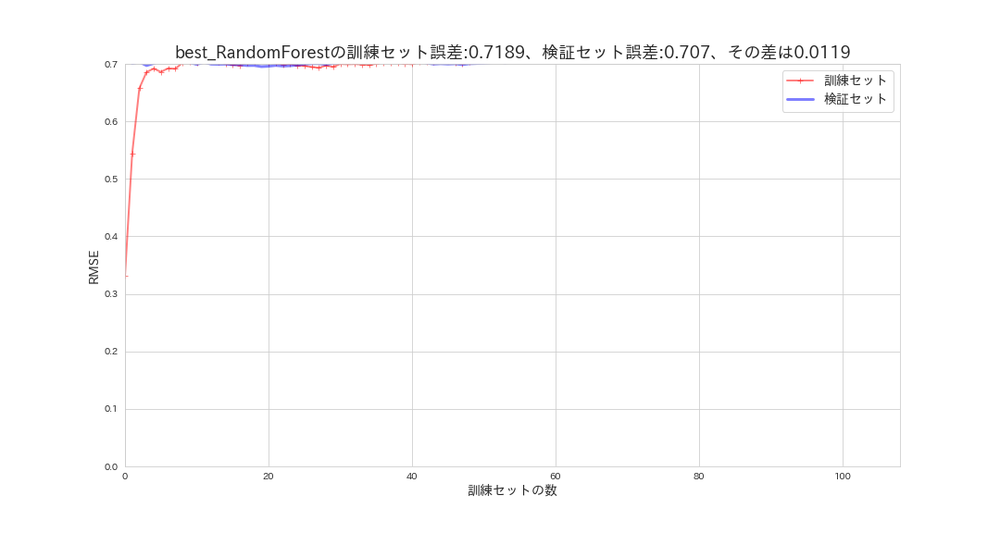
訓練誤差と検証誤差の誤差を見る限り、かなり汎化性能は高くなりましたがグラフの範囲外に隠れてしまいました。残念です。
GradientBoostingTree(ランダムサーチ)の学習曲線¶
所要時間約1分(CPU)
# max_depth: 最大ノード数(正則化)
# n_estimators: 決定木の個数
random_search = {'max_depth': [1, 2],
'n_estimators': [300, 500, 1000, 2000],
'random_state': [42]}
gb_reg = GradientBoostingRegressor()
gb_random_search = RandomizedSearchCV(gb_reg,
random_search,
cv=5,
n_jobs=-1,
scoring='neg_mean_squared_error',
n_iter=8,
random_state=42)
gb_random_search.fit(X_s, y)
gb_random_search.best_params_
# 結果
{'random_state': 42, 'n_estimators': 2000, 'max_depth': 2}
所要時間約5分(CPU)
# 実行
plot_learning_curves(gb_random_search.best_estimator_, X_s, y, model_name='best_GBoost')
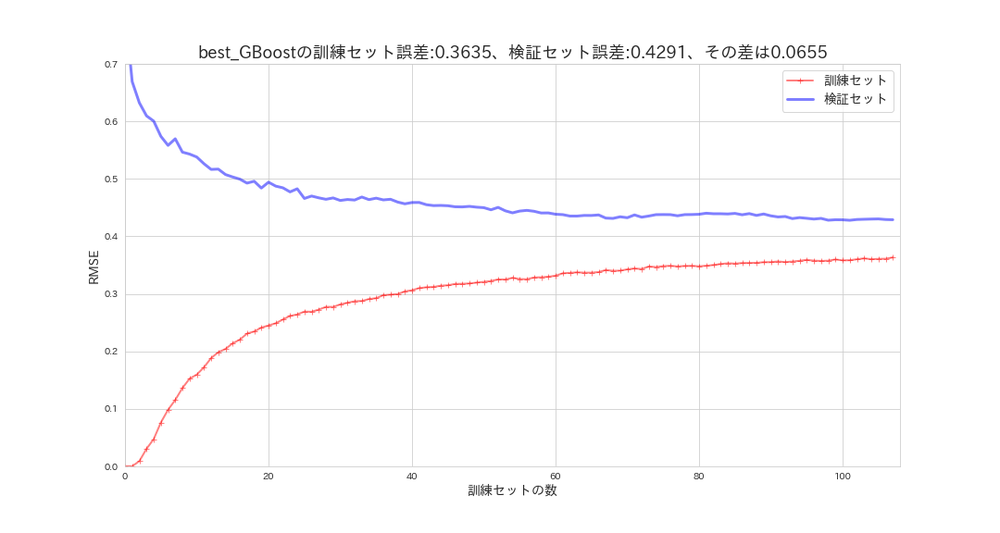
デフォルトの設定と比べて性能は上がりましたが、汎化性能は今一低いようです。
MLP(ランダムサーチ)の学習曲線¶
所要時間約22分(CPU)
# hidden_layer_sizes: ニューロンと層の数
# learning_rate_init: 重みを更新するステップサイズの制御
# max_iter: エポック数
# epsilon: ReLuの正則化ハイパーパラメータ値
random_search = {'hidden_layer_sizes': [(100),
(100, 100),
(20, 30, 50, 30, 20),
(20, 50, 80, 50, 20),
(20, 100, 100, 100, 20)],
'learning_rate_init': [0.1, 0.01, 0.001, 0.0001],
'epsilon': [0.01, 0.1, 0.2, 1],
'max_iter': [1500],
'random_state': [42]}
mlp_reg = MLPRegressor()
mlp_random_search = RandomizedSearchCV(mlp_reg,
random_search,
cv=5,
n_jobs=-1,
scoring='neg_mean_squared_error',
n_iter=20,
random_state=42)
mlp_random_search.fit(X_s, y)
mlp_random_search.best_params_
# 結果
{'random_state': 42,
'max_iter': 1500,
'learning_rate_init': 0.001,
'hidden_layer_sizes': (20, 30, 50, 30, 20),
'epsilon': 0.01}
所要時間約28分(CPU)
# 実行
plot_learning_curves(mlp_random_search.best_estimator_, X_s, y, model_name='best_MLP')
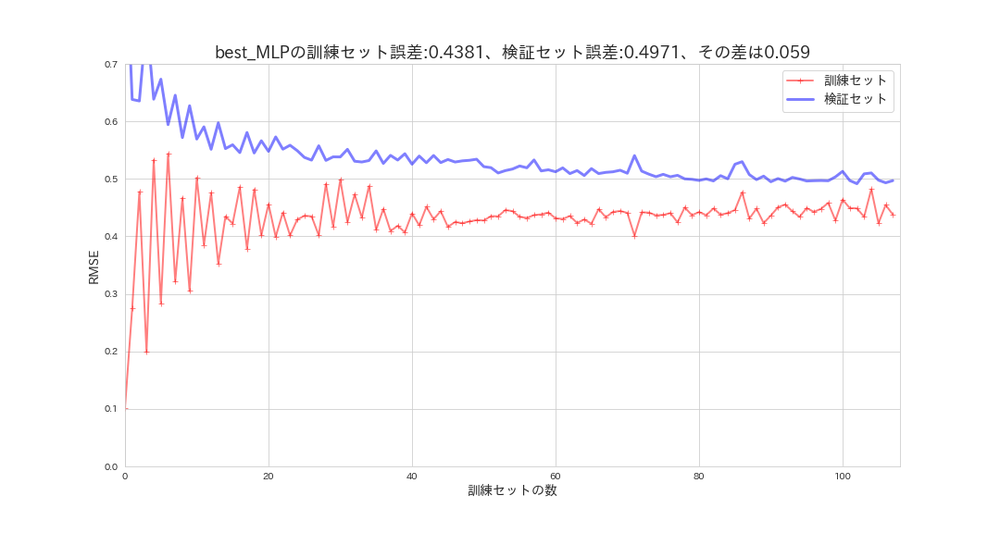
デフォルト設定と比べて、余り変化はありませんが、訓練セットに適合し過ぎてしまっている様子です。
ではデフォルト設定とランダムサーチ後の設定で、訓練誤差と検証誤差の誤差を比べてみましょう。
# 実行
df_error['Random_Search'] = generalization_error
df_error
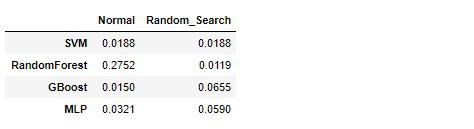
RandomForestは残念ながら正則化を強めたら性能自体悪くなってしまいました。
それ以外のモデルで、誤差の最小範囲にだけ注目するならば、デフォルト設定のSVMもしくわGradientBoostingTreeが最良の候補に挙がります。
もう一度双方の学習曲線の見比べて判断してみます。
グラフを描画する際に、plt.savefig()にて画像を保存しているので、matplotlibを使って表示させます。
※見え難い画像ですがご了承ください。
SVMの学習曲線
# 実行
svm_img = plt.imread('SVM_error.png')
plt.figure(figsize=(15, 12))
plt.imshow(svm_img)
plt.savefig('imshow_svm.png')
plt.show()
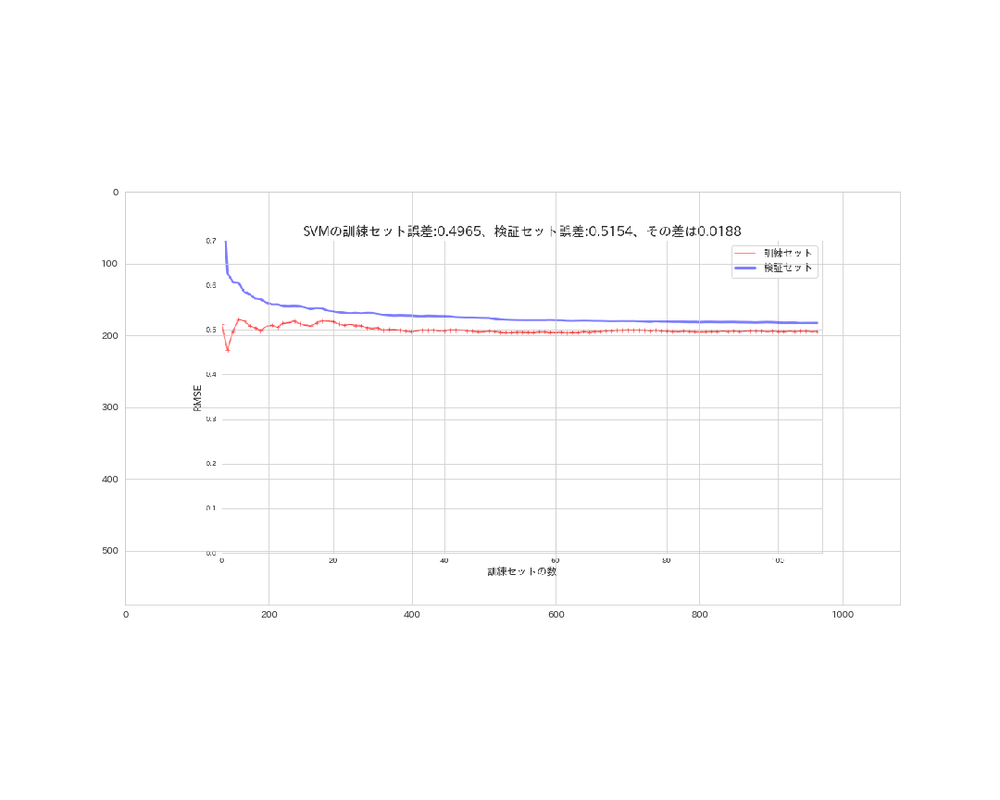
GradientBoostingTreeの学習曲線
# 実行
gb_img = plt.imread('GBoost_error.png')
plt.figure(figsize=(15, 12))
plt.imshow(gb_img)
plt.savefig('imshow_gb.png')
plt.show()
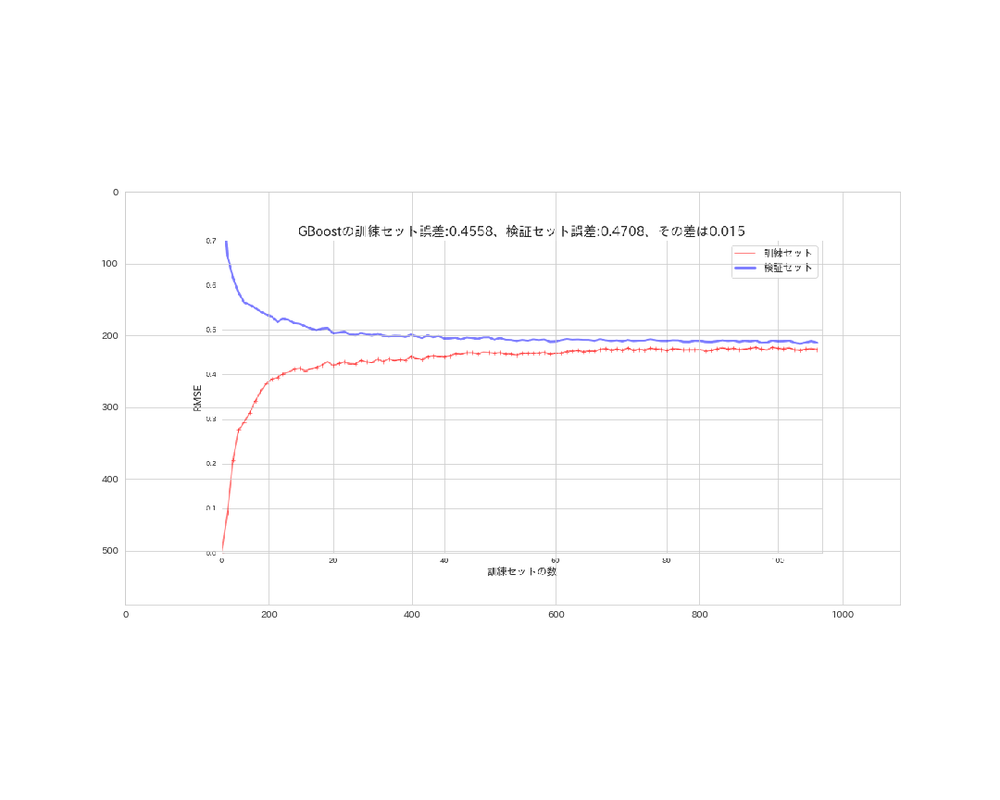
グラフや誤差を見ても、総合的にデフォルト設定のGradientBoostingTreeが最も最良なモデルであると判断できるので、ここではこのモデルを採用したいと思います。
テストセットの評価¶
gb_reg.fit(X_s, y)
X_test, y_test = custom_conversion(test_set)
# スケーリング
X_test_s = scaler.transform(X_test)
best_model_pred = gb_reg.predict(X_test_s)
best_model_mse = mean_squared_error(y_test, best_model_pred)
best_model_rmse = np.sqrt(best_model_mse)
best_model_rmse
# 結果
0.4783415877004818
訓練セットのRMSEを確認してみます。
# 実行
train_model_pred = gb_reg.predict(X_s)
train_model_mse = mean_squared_error(y, train_model_pred)
train_model_rmse = np.sqrt(train_model_mse)
train_model_rmse
# 結果
0.4628402048901585
GradientBoostingTreeはハイパーパラメータがデフォルト設定でもかなり汎化性能が高いモデルであると言えます。
学習曲線を見ても、訓練セットと検証セットはデータが増えることにより差が縮まっています。
GradientBoostingTreeは上手くデータに適合されていましたが、過学習モデルの汎化性能を上げるためには、訓練データを増やせば改善される可能性があるという事です。
データが無いのであれば、正則化を強めたり、単純なモデルに切り替えたりすることで過学習を抑えられます。
やはり一番重要になってくるのは「データ」です。
クリーンなデータが多ければ多いほど、機械学習の本領も発揮されます。
最良のモデルとスケーラーをpickleファイルに保存¶
最後に、本番稼働用にモデルを使えるようにするため、pickleファイルに保存しておきます。
本番では生データが読み込まれるので、訓練セットに適合されたスケーラーを使えるようにするために、スケーラーオブジェクトも保存します。
import pickle
# モデルの保存
# 前回のモデルと被らないために、best_model_2とする
with open('best_model_2.pickle', 'wb') as f:
pickle.dump(gb_reg, f)
# スケーラーの保存
with open('scaler.pickle', 'wb') as f:
pickle.dump(scaler, f)
保存したモデルの読み込みは
# 実行
with open('best_model_2.pickle', 'rb') as f:
best_model_2 = pickle.load(f)
best_model_2
# 結果
GradientBoostingRegressor(alpha=0.9, criterion='friedman_mse', init=None,
learning_rate=0.1, loss='ls', max_depth=3,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_iter_no_change=None, presort='auto',
random_state=42, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
課題¶
無事に、最良のモデルを選び出すことができたので、次の課題は本番稼働するためにシステムを構築し与えられたデータに対して予測を実行できるようにすることです。
- オンラインでも実行可能なWebアプリケーションを構築
- 環境構築(必要なライブラリをインストールする)
- 開発
- 試行
それでは以上となります。
最後までご覧いただきありがとうございました。
